Goniometry and trigonometry - math word problems - page 12 of 32
Number of problems found: 628
- Isosceles trapezoid
 Find the height in an isosceles trapezoid if the area is 520 cm² and the base a = 25 cm and c = 14 cm. Calculate the interior angles of the trapezoid.
Find the height in an isosceles trapezoid if the area is 520 cm² and the base a = 25 cm and c = 14 cm. Calculate the interior angles of the trapezoid. - Cosine
 Cosine and sine theorem: Calculate all unknown values (side lengths or angles) from triangle ABC. c = 2.9 cm; β = 28°; γ = 14° α =? °; a =? cm; b =? cm
Cosine and sine theorem: Calculate all unknown values (side lengths or angles) from triangle ABC. c = 2.9 cm; β = 28°; γ = 14° α =? °; a =? cm; b =? cm - Diagonal BD
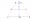 Find the length of the diagonal BD in a rectangular trapezoid ABCD with a right angle at vertex A when/AD / = 8,1 cm and the angle DBA is 42°
Find the length of the diagonal BD in a rectangular trapezoid ABCD with a right angle at vertex A when/AD / = 8,1 cm and the angle DBA is 42° - Parallelogram
 Find the parallelogram's perimeter, where base a = 8 cm, height v = 3 cm, and angle alpha = 35° is the magnitude of the angle at vertex A.
Find the parallelogram's perimeter, where base a = 8 cm, height v = 3 cm, and angle alpha = 35° is the magnitude of the angle at vertex A. - TV tower
 Calculate the height of the television tower if an observer standing 430 m from the base of the tower sees the peak at an altitude angle of 23°.
Calculate the height of the television tower if an observer standing 430 m from the base of the tower sees the peak at an altitude angle of 23°. - Triangle ABC v2
 The area of the triangle is 12 cm square. Angle ACB = 30º , AC = (x + 2) cm, BC = x cm. Calculate the value of x.
The area of the triangle is 12 cm square. Angle ACB = 30º , AC = (x + 2) cm, BC = x cm. Calculate the value of x. - Circumference 26361
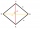 The ABCD diamond has a circumference of 72 cm. The longer diagonal of the animal with the line segment AB angle is 30 °. Calculate the area of the ABCD diamond.
The ABCD diamond has a circumference of 72 cm. The longer diagonal of the animal with the line segment AB angle is 30 °. Calculate the area of the ABCD diamond. - Trigonometric 50551
 Solve the trigonometric equation: cos (x-52°) = 1
Solve the trigonometric equation: cos (x-52°) = 1 - Pentadecagon
 Calculate the area of a regular 15-side polygon inscribed in a circle with a radius r = 4. Express the result to two decimal places.
Calculate the area of a regular 15-side polygon inscribed in a circle with a radius r = 4. Express the result to two decimal places. - Two chords
 From the point on the circle with a diameter of 8 cm, two identical chords are led, which form an angle of 60°. Calculate the length of these chords.
From the point on the circle with a diameter of 8 cm, two identical chords are led, which form an angle of 60°. Calculate the length of these chords. - A rhombus
 A rhombus has sides of the length of 10 cm, and the angle between two adjacent sides is 76 degrees. Find the length of the longer diagonal of the rhombus.
A rhombus has sides of the length of 10 cm, and the angle between two adjacent sides is 76 degrees. Find the length of the longer diagonal of the rhombus. - Roof angle
 The house's roof has the shape of an isosceles triangle with arms 4 m long and the size of the base 6 m. How big an angle alpha does its roof make?
The house's roof has the shape of an isosceles triangle with arms 4 m long and the size of the base 6 m. How big an angle alpha does its roof make? - Degrees 70334
 What is the height of a diamond with a side 6 cm long if the angle formed by the sides is 78 degrees and 10 '?
What is the height of a diamond with a side 6 cm long if the angle formed by the sides is 78 degrees and 10 '? - Calculate 3209
 Calculate the lengths of the sides of the triangle ABC, in which angles α = 113°, β = 48°, and the radius of the circle of the triangle described is r = 10 cm.
Calculate the lengths of the sides of the triangle ABC, in which angles α = 113°, β = 48°, and the radius of the circle of the triangle described is r = 10 cm. - ABS, ARG, CONJ, RECIPROCAL
 Let z=-√2-√2i where i2 = -1. Find |z|, arg(z), z* (where * indicates the complex conjugate), and (1/z). Where appropriate, write your answers in the form a + i b, where both a and b are real numbers. Indicate the positions of z, z*, and (1/z) on an Argand
Let z=-√2-√2i where i2 = -1. Find |z|, arg(z), z* (where * indicates the complex conjugate), and (1/z). Where appropriate, write your answers in the form a + i b, where both a and b are real numbers. Indicate the positions of z, z*, and (1/z) on an Argand - goniometric functions
 Based on the fact that you know the values of sin and cos of a given angle and you know that tan (tangent) is their ratio, determine d) tan 120 ° e) tan 330 °
Based on the fact that you know the values of sin and cos of a given angle and you know that tan (tangent) is their ratio, determine d) tan 120 ° e) tan 330 ° - Tree
 Between points A and B is 50m. From A, we see a tree at an angle of 18°. From point B, we see the tree at a three times bigger angle. How tall is a tree?
Between points A and B is 50m. From A, we see a tree at an angle of 18°. From point B, we see the tree at a three times bigger angle. How tall is a tree? - Horizontal 64864
 The meter stick is located on the meridian plane and deviated from the horizontal plane to the north by an angle of magnitude 70°. Calculate the length of the shadow cast by a meter stick at true noon if the Sun culminates at an angle of 41°03'.
The meter stick is located on the meridian plane and deviated from the horizontal plane to the north by an angle of magnitude 70°. Calculate the length of the shadow cast by a meter stick at true noon if the Sun culminates at an angle of 41°03'. - Course to airport
 The plane flew from airport m on a course of 132° to airport n, then from n to p on a course of 235°. The distance between the airport's mn is 380 km, np 284 km. What will be the return course to m, and what is the distance between the airport's pm?
The plane flew from airport m on a course of 132° to airport n, then from n to p on a course of 235°. The distance between the airport's mn is 380 km, np 284 km. What will be the return course to m, and what is the distance between the airport's pm? - Calculate 3208
 Calculate the size of the sides and angles of the triangle ABC if you know vc = 28, α = 51 ° 19 ', β = 67 ° 38'.
Calculate the size of the sides and angles of the triangle ABC if you know vc = 28, α = 51 ° 19 ', β = 67 ° 38'.
Do you have homework that you need help solving? Ask a question, and we will try to solve it. Solving math problems.
