Goniometry and trigonometry - math word problems - page 18 of 32
Number of problems found: 624
- Calculate 6219
Right triangle. Given: side b = 15.8 angle alpha = 15° 11`. Calculate the side a, c, beta angle, and area. - Complex roots
Find the sum of the fourth square root of the number 16. - Circular segment
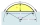A circular segment has an area of 6.04 cm², the central omega angle is 15 degrees, what is the radius? - Area 51
The area of the triangle is 54.39, alpha is 32 °, and gamma is 144 °. - Calculate roots of z
Calculate the ratio of the two fifth roots of the number 32. - Sin cos tan
If cos y = 0.8, 0° ≤ y ≤ 90°, find the value of (4 tan y) / (cos y-sin y) - Calculate 2
Calculate the largest angle of the triangle whose sides are 5.2cm, 3.6cm, and 2.1cm - Trigonometry
If you know that cos(γ) = sin (806°), what is the angle γ? - Determine 82034
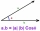The vectors a = (3, -2), b = (-1, 5) are given. Determine the vector c for which a. c = 17; c = 3 - Scalar dot product
Calculate u.v if |u| = 5, |v| = 2 and when the angle between the vectors u, v is: a) 60° b) 45° c) 120° - A ship
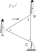A ship has been spotted by two lighthouses, A and B, as shown in the figure. What is the distance from the ship to Lighthouse A to the nearest tenth? Figure - the distance between lighthouses A and B is 40 nautical miles. From A is seen in view angle 57° - Directional 2595
Calculate the interior angles of triangle ABC using vectors. Coordinates A [2; 4] B [4; 6] C [0; -4]. Calculate directional vectors of sides, parametric and general equations of sides, parametric and general equations of lines, calculate area, calculate h - Central angle
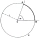A circle k with a center at point S and a radius of 6 cm is given. Calculate the size of the central angle subtended by a chord 10 cm long. - Determine 8133
Determine the distance between two places, M, and N, between which there is an obstacle so that place N is not visible from place M. The angles MAN = 130°, NBM = 109°, and the distances |AM| = 54, |BM| = 60, while the points A, B, and M lie on one straigh - Trapezoid IV
In a trapezoid ABCD (AB||CD) is |AB| = 15cm |CD| = 7 cm, |AC| = 12 cm, AC is perpendicular to BC. What area has a trapezoid ABCD? - Forces
Forces with magnitudes F1 = 42N and F2 = 35N act at a common point and make an angle of 77°12'. How big is their resultant? - Triangle
Plane coordinates of vertices: K[9, 5] L[-4, 8] M[3, 20] give Triangle KLM. Calculate its area and its interior angles. - Maturitný - RR - base
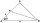In an isosceles triangle ABC with base AB, ∠BAC = 20°, AB = 4. The axis of the interior angle at vertex B intersects side AC at point P. Calculate the length of the segment AP. Give the result to two decimal places. - Cosine
Calculate the cosine of the smallest internal angle in a right-angled triangle with cathetus 3 and 8 and the hypotenuse 8.544. - Climb
The road has climbing 1:28. How big is the angle that corresponds to this climbing?
Do you have homework that you need help solving? Ask a question, and we will try to solve it. Solving math problems.
