Goniometry and trigonometry - math word problems - page 19 of 32
Number of problems found: 629
- Height of poplar
 From the 40 m high observation deck, you can see the top of the poplar at a depth angle of 50°10' and the bottom of the poplar at a depth angle of 58°. Calculate the height of the poplar.
From the 40 m high observation deck, you can see the top of the poplar at a depth angle of 50°10' and the bottom of the poplar at a depth angle of 58°. Calculate the height of the poplar. - Bearing - navigation
 A ship travels 84 km on a bearing of 17° and then travels on a bearing of 107° for 135 km. Find the distance of the end of the trip from the starting point to the nearest kilometer.
A ship travels 84 km on a bearing of 17° and then travels on a bearing of 107° for 135 km. Find the distance of the end of the trip from the starting point to the nearest kilometer. - Approximation of tangent fx
 What is the nontrigonometric formula (not a polynomial fit) for the growth curve that solves algebraically for the increase between tan(1 degree) and tan(2 degrees) continuing up to the tangent(45 degrees)? Okay, to use pi Check calculation for 12°.
What is the nontrigonometric formula (not a polynomial fit) for the growth curve that solves algebraically for the increase between tan(1 degree) and tan(2 degrees) continuing up to the tangent(45 degrees)? Okay, to use pi Check calculation for 12°. - V-belt
 Calculate the length of the V-belt when the diameter of the pulleys is: D1 = 600 mm D2 = 120 mm d = 480 mm (distance between pulley axes)
Calculate the length of the V-belt when the diameter of the pulleys is: D1 = 600 mm D2 = 120 mm d = 480 mm (distance between pulley axes) - Angle
 A straight line p given by the equation y = (-8)/(3) x (+)76. Calculate the size of the angle in degrees between line p and y-axis.
A straight line p given by the equation y = (-8)/(3) x (+)76. Calculate the size of the angle in degrees between line p and y-axis. - View angle
 At a distance of 10 m from the river bank, they measured the base AB = 50 m parallel to the bank. Point C on the other bank of the river is visible from point A at an angle of 32°30' and from point B at an angle of 42°15'. Calculate the width of the river
At a distance of 10 m from the river bank, they measured the base AB = 50 m parallel to the bank. Point C on the other bank of the river is visible from point A at an angle of 32°30' and from point B at an angle of 42°15'. Calculate the width of the river - Tangens parallelogram
 If ∠BAD between the sides AB and AD of the parallelogram is θ, what is tan θ? See diagram: A=(7,1) B=(5,-2) C=(12,1) D=(14,4)
If ∠BAD between the sides AB and AD of the parallelogram is θ, what is tan θ? See diagram: A=(7,1) B=(5,-2) C=(12,1) D=(14,4) - Mast shadow
 The mast has a 13 m long shadow on a slope rising from the mast foot toward the shadow angle at an angle of 15°. Determine the height of the mast if the sun above the horizon is at an angle of 33°. Use the law of sines.
The mast has a 13 m long shadow on a slope rising from the mast foot toward the shadow angle at an angle of 15°. Determine the height of the mast if the sun above the horizon is at an angle of 33°. Use the law of sines. - Line coefficient determination
 In the equation of the line p: ax-2y+1=0, determine the coefficient a so that the line p: a) it formed an angle of 120° with the positive direction of the x-axis, b) passed through point A[3,-2], c) was parallel to the x-axis, d) had a direction of k = 4.
In the equation of the line p: ax-2y+1=0, determine the coefficient a so that the line p: a) it formed an angle of 120° with the positive direction of the x-axis, b) passed through point A[3,-2], c) was parallel to the x-axis, d) had a direction of k = 4. - In plane 2
 A triangle ABC is located in the plane with a right angle at vertex C, for which the following holds: A(1, 2), B(5, 2), C(x, x+1), where x > -1. a) determine the value of x b) determine the coordinates of point M, which is the midpoint of line segment
A triangle ABC is located in the plane with a right angle at vertex C, for which the following holds: A(1, 2), B(5, 2), C(x, x+1), where x > -1. a) determine the value of x b) determine the coordinates of point M, which is the midpoint of line segment - Triangle
 Plane coordinates of vertices: K[9, 5] L[-4, 8] M[3, 20] give Triangle KLM. Calculate its area and its interior angles.
Plane coordinates of vertices: K[9, 5] L[-4, 8] M[3, 20] give Triangle KLM. Calculate its area and its interior angles. - A boy
 A boy of 1.7m in height is standing 30m away from the flagstaff on the same level ground. He observes that the angle of deviation of the top of the flagstaff is 30 degrees. Calculate the height of the flagstaff.
A boy of 1.7m in height is standing 30m away from the flagstaff on the same level ground. He observes that the angle of deviation of the top of the flagstaff is 30 degrees. Calculate the height of the flagstaff. - Length of the chord
 Calculate the length of the chord in a circle with a radius of 25 cm and a central angle of 26°.
Calculate the length of the chord in a circle with a radius of 25 cm and a central angle of 26°. - Slope of the pool
 Calculate the slope (ratio rise:run) of the bottom of the swimming pool long 40 m. The water depth at the beginning of the pool is 1.09 m (for children), and the depth at the end is 1.88 m (for swimmers). Calculated slope write it as a percentage and also
Calculate the slope (ratio rise:run) of the bottom of the swimming pool long 40 m. The water depth at the beginning of the pool is 1.09 m (for children), and the depth at the end is 1.88 m (for swimmers). Calculated slope write it as a percentage and also - Unit circle
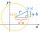 In the Cartesian coordinate system, a unit circle is given on which points A and B lie. Point O is the origin and has coordinates (0,0) and point B has coordinates (1,0). The size of angle BOA is 151°. Determine the x-coordinate of point A.
In the Cartesian coordinate system, a unit circle is given on which points A and B lie. Point O is the origin and has coordinates (0,0) and point B has coordinates (1,0). The size of angle BOA is 151°. Determine the x-coordinate of point A. - Rhombus
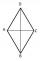 ABCD is a rhombus, ABD is an equilateral triangle, and AC is equal to 4. Find the area of the rhombus.
ABCD is a rhombus, ABD is an equilateral triangle, and AC is equal to 4. Find the area of the rhombus. - Trapezoid IV
 In a trapezoid ABCD (AB||CD) is |AB| = 15cm |CD| = 7 cm, |AC| = 12 cm, AC is perpendicular to BC. What area has a trapezoid ABCD?
In a trapezoid ABCD (AB||CD) is |AB| = 15cm |CD| = 7 cm, |AC| = 12 cm, AC is perpendicular to BC. What area has a trapezoid ABCD? - Tower's view
 From the church tower's view at 65 m, the top of the house can be seen at a depth angle of alpha = 45° and its bottom at a depth angle of beta = 58°. Calculate the house's height and its distance from the church.
From the church tower's view at 65 m, the top of the house can be seen at a depth angle of alpha = 45° and its bottom at a depth angle of beta = 58°. Calculate the house's height and its distance from the church. - Hexagonal prism angle
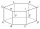 The given is a regular hexagonal prism ABCDEFGHIJKL, which has all edges of the same length. Find the degree of the angle formed by the lines BK and CL in degrees.
The given is a regular hexagonal prism ABCDEFGHIJKL, which has all edges of the same length. Find the degree of the angle formed by the lines BK and CL in degrees. - Climb
 The road has climbing 1:28. How big is the angle that corresponds to this climbing?
The road has climbing 1:28. How big is the angle that corresponds to this climbing?
Do you have unsolved math question and you need help? Ask a question, and we will try to solve it. We solve math question.
