Planimetrics - math word problems - page 133 of 185
Number of problems found: 3684
- Diagonals at right angle
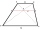 In the trapezoid ABCD, this is given: AB=12cm CD=4cm And diagonals crossed under a right angle. What is the area of this trapezoid ABCD?
In the trapezoid ABCD, this is given: AB=12cm CD=4cm And diagonals crossed under a right angle. What is the area of this trapezoid ABCD? - Percentage - rhombus
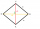 If the rhombus side in the image increases by half, by what percentage will the area of the rhombus increase?
If the rhombus side in the image increases by half, by what percentage will the area of the rhombus increase? - Rectangle - WL in ratio
 Find the length of a rectangle if the width is 28 cm and the length and width are in the ratio 7:4 (l:w).
Find the length of a rectangle if the width is 28 cm and the length and width are in the ratio 7:4 (l:w). - It is rectangular?
 The size of two of the angles in a triangle is α=110°, β=40°. Is it a right triangle?
The size of two of the angles in a triangle is α=110°, β=40°. Is it a right triangle? - Successive 45281
 The sizes of the interior angles of the triangle are in a successive ratio of 6:4:5 are these angles big?
The sizes of the interior angles of the triangle are in a successive ratio of 6:4:5 are these angles big? - Largest squares
 How many of the largest square sheets did the plumber cut the honeycomb from 16 dm and 96 dm?
How many of the largest square sheets did the plumber cut the honeycomb from 16 dm and 96 dm? - The parabolic segment
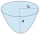 The parabolic segment has a base a = 4 cm and a height v = 6 cm. Calculate the volume of the body that results from the rotation of this segment a) around its base b) around its axis.
The parabolic segment has a base a = 4 cm and a height v = 6 cm. Calculate the volume of the body that results from the rotation of this segment a) around its base b) around its axis. - A rectangle 2
 A rectangle has a diagonal length of 74cm. Its side lengths are in a ratio of 5:3. Find its side lengths.
A rectangle has a diagonal length of 74cm. Its side lengths are in a ratio of 5:3. Find its side lengths. - Isosceles trapezoid
 Calculate the area of an isosceles trapezoid whose bases are in the ratio of 4:3; leg b = 13 cm and height = 12 cm.
Calculate the area of an isosceles trapezoid whose bases are in the ratio of 4:3; leg b = 13 cm and height = 12 cm. - Calculate 73024
 Calculate the permille descent of the railway line in the section of 7.2 km by 21.6 m.
Calculate the permille descent of the railway line in the section of 7.2 km by 21.6 m. - Similarity
 The area of the regular 5-gon is 495 cm². The area of similar 5-gon is 606 dm². What is the coefficient of similarity?
The area of the regular 5-gon is 495 cm². The area of similar 5-gon is 606 dm². What is the coefficient of similarity? - Approximately 20243
 Lake Trasimeno is approximately in the shape of a circle, its area is about 28 square kilometers, and Mr. Hector's walking speed is approximately 4km/h. Calculate the length of the path around the lake and how many hours Mr. Hector would have to walk to o
Lake Trasimeno is approximately in the shape of a circle, its area is about 28 square kilometers, and Mr. Hector's walking speed is approximately 4km/h. Calculate the length of the path around the lake and how many hours Mr. Hector would have to walk to o - Right-angled 81019
 In the right-angled triangle ABC (AB is the hypotenuse), a : b = 24 : 7, and the height to the side c = 12.6 cm applies. Calculate the lengths of the sides of triangle ABC.
In the right-angled triangle ABC (AB is the hypotenuse), a : b = 24 : 7, and the height to the side c = 12.6 cm applies. Calculate the lengths of the sides of triangle ABC. - Clock hands
 The hands-on clock shows the time as 12 hours and 2 minutes. Three hours later, calculate the size of an acute angle between the clock hands.
The hands-on clock shows the time as 12 hours and 2 minutes. Three hours later, calculate the size of an acute angle between the clock hands. - RT and ratio
 A right triangle whose legs are in a ratio 7:14 has a hypotenuse 79 m long. How long are its legs?
A right triangle whose legs are in a ratio 7:14 has a hypotenuse 79 m long. How long are its legs? - Aircraft bearing
 Two aircraft will depart from the airport simultaneously. The first flight flies with a course of 30°, and the second with a course of 86°. Both fly at 330 km/h. How far apart will they be in 45 minutes of flight?
Two aircraft will depart from the airport simultaneously. The first flight flies with a course of 30°, and the second with a course of 86°. Both fly at 330 km/h. How far apart will they be in 45 minutes of flight? - Perpendicular 5712
 Adam and Boris go from school on two perpendicular paths. Adam's average speed is 6 km/h, and Borisova's is 8 km/h. How far will they be by air for 0.5 hours?
Adam and Boris go from school on two perpendicular paths. Adam's average speed is 6 km/h, and Borisova's is 8 km/h. How far will they be by air for 0.5 hours? - Rectangular 80776
 The perimeter of the rectangular garden is 42 meters. Its sides are in the ratio 3:4. Calculate the length of the sidewalk that is the diagonal of the garden.
The perimeter of the rectangular garden is 42 meters. Its sides are in the ratio 3:4. Calculate the length of the sidewalk that is the diagonal of the garden. - Rhombus - ratio
 In a rhombus, the ratio of the side to the height to this side is 4 : 1, if its area is 49 cm². Calculate the size of the side and the height to this side.
In a rhombus, the ratio of the side to the height to this side is 4 : 1, if its area is 49 cm². Calculate the size of the side and the height to this side. - Half of halves
 We cut half of the square off, then half of the rest, etc. Five cuts we made in this way. What part of the area of the original square is the area of the cut part?
We cut half of the square off, then half of the rest, etc. Five cuts we made in this way. What part of the area of the original square is the area of the cut part?
Do you have unsolved math question and you need help? Ask a question, and we will try to solve it. We solve math question.
