Planimetrics - math word problems - page 142 of 185
Number of problems found: 3688
- An electrician 3
In setting up a wiring job, an electrician ran the following lengths of wire: 340 m, 203 m, 74 m, and 99 m. Find the total length of wire used. - Clock Tower
What angle is between the hands-on Clock Tower when it shows 17 hours and 35 minutes? - Proof PT
Can you easily prove Pythagoras' theorem using Euclidean theorems? If so, do it. - Garage
There are two laths in the garage opposite one another: one 2 meters long and the second 3 meters long. They fall against each other and stay against the opposite walls of the garage. Both laths cross 70 cm above the garage floor. How wide is the garage? - Area of RT
Calculate the right triangle area in which the hypotenuse has length 14 and one hypotenuse segment has length 5. - Building shadow length
How long a shadow casts a building 15 m high if the shadow of a meter rod is 90 cm? Sketch - similarity. - Snowman column shadow
Under the column, the children built a 1.65m tall snowman. The snowman's shadow is 135 cm long. The shadow of the column has a length of 4.05 m. How tall is the pole? - Poplar shadow
The nine-meter poplar casts a shadow 16.2 m long. How long does a shadow cast by Peter at the same time if it is 1.4 m high? - Chimney and tree Calculate the height of the factory chimney, which casts a shadow of 6.5 m long in the afternoon. At the same time, a 6 m high tree standing near it casts a shadow 25 dm long.
- Display case
Place a glass shelf at the height of 1m from the bottom of the display case in the cabinet. How long platter will we place at this height? The display case is a rectangular triangle with 2 m and 2.5 m legs. - Chimney shadow height
At the same time, a vertical 2-meter pole casts a shadow of 0.85 meters. At the same time, a chimney of unknown height casts a 45m long shadow. Determine the height of the chimney. - Triangle similarity decision
Decide whether the triangles are similar. Choose between Yes/No. ∆ YUO: y= 9m, u= 17 m, o= 12 m, ∆ ZXV= z= 207 dm, x= 341 dm, v= 394 dm - Triangle similarity area
Triangle ABC and triangle ADE are similar. Calculate in square centimeters the area of triangle ABC if the length of side DE is 12 cm, the length of side BC is 16 cm, and the area of triangle ADE is 27 cm². - Shadow
A meter pole perpendicular to the ground throws a shadow of 40 cm long. The house throws a shadow 6 meters long. What is the height of the house? - Diagonals
What x-gon has 54 diagonals? - Laws
From which law directly follows the validity of Pythagoras' theorem in the right triangle? ... - Area of RT
The right triangle has orthogonal projections of legs to the hypotenuse lengths 15 cm and 9 cm. Determine the area of this triangle. - Clock quadrilateral angle
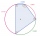Calculate the magnitude of the largest inner angle and the deviation of the diagonals in the quadrilateral, whose vertices correspond to points 1, 5, 8, and 12 on the dial. - Triangle circle area
A right isosceles triangle is inscribed in the circle with r = 8 cm. Find triangle area S. How much percent does the triangle occupy the area of the circle? - Tree height
A tree with an unknown height casts a shadow 18 m long at a time, while a two-meter pole casts a shadow of 2.4 m. How tall is the tree?
Do you have homework that you need help solving? Ask a question, and we will try to solve it. Solving math problems.
