Planimetrics - math word problems - page 141 of 185
Number of problems found: 3685
- Triangle
 In triangle ABC, there is a point S with the center of the inscribed circle. The area of quadrilateral ABCS is equal to four-fifths of the area of triangle ABC. The lengths of the sides of triangle ABC expressed in centimeters are all integers and the
In triangle ABC, there is a point S with the center of the inscribed circle. The area of quadrilateral ABCS is equal to four-fifths of the area of triangle ABC. The lengths of the sides of triangle ABC expressed in centimeters are all integers and the - Square garden
 The plan with a scale of 1:1500 is drawn as a square garden with an area 64 cm². How many meters is the garden fence long? Determine the actual acreage gardens.
The plan with a scale of 1:1500 is drawn as a square garden with an area 64 cm². How many meters is the garden fence long? Determine the actual acreage gardens. - Similarity coefficient
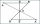 In the triangle TMA, the length of the sides is t = 5cm, m = 3.5cm, and a = 6.2cm. Another similar triangle has side lengths of 6.65 cm, 11.78 cm, and 9.5 cm. Determine the similarity coefficient of these triangles and assign similar sides to each other.
In the triangle TMA, the length of the sides is t = 5cm, m = 3.5cm, and a = 6.2cm. Another similar triangle has side lengths of 6.65 cm, 11.78 cm, and 9.5 cm. Determine the similarity coefficient of these triangles and assign similar sides to each other. - The observer - trees
 The observer sees the tops of two trees at the same angle α. It is 9 m from one tree and 21 m from the other. The trees stand on a level. How tall is the second tree if the height of the first is 6 m? Remember that the eyes of a standing person are approx
The observer sees the tops of two trees at the same angle α. It is 9 m from one tree and 21 m from the other. The trees stand on a level. How tall is the second tree if the height of the first is 6 m? Remember that the eyes of a standing person are approx - Shadow of tree
 Miro stands under a tree and watches its shadow and shadow of the tree. Miro is 180 cm tall, and its shade is 1.5 m long. The tree's shadow is three times as long as Miro's shadow. How tall is the tree in meters?
Miro stands under a tree and watches its shadow and shadow of the tree. Miro is 180 cm tall, and its shade is 1.5 m long. The tree's shadow is three times as long as Miro's shadow. How tall is the tree in meters? - Rhombus construction
 Construct ABCD rhombus if its diagonal AC=9 cm and side AB = 6 cm. Inscribe a circle in it, touching all sides.
Construct ABCD rhombus if its diagonal AC=9 cm and side AB = 6 cm. Inscribe a circle in it, touching all sides. - Actually 83215
 The square-shaped plot actually covers an area of 81 ares. Maybe draw it in the village plan on a scale of 1:200. What will be the length of the side on the plan?
The square-shaped plot actually covers an area of 81 ares. Maybe draw it in the village plan on a scale of 1:200. What will be the length of the side on the plan? - Squares above sides
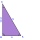 In a right triangle, the areas of the squares above its sides are 169, 25, and 144. The length of its longer leg is:
In a right triangle, the areas of the squares above its sides are 169, 25, and 144. The length of its longer leg is: - Motorcycle 5354
 The diameter of the motorcycle wheel is 60 cm. How many times does the wheel turn on a track 1,884 km long?
The diameter of the motorcycle wheel is 60 cm. How many times does the wheel turn on a track 1,884 km long? - Snowman's 82155
 Under the column, the children built a 1.65m tall snowman. The snowman's shadow is 135 cm long. The shadow of the column has a length of 4.05 m. How tall is the pole?
Under the column, the children built a 1.65m tall snowman. The snowman's shadow is 135 cm long. The shadow of the column has a length of 4.05 m. How tall is the pole? - Rectangular triangles
 The lengths of the corresponding sides of two rectangular triangles are in the ratio 2:5. At what ratio are medians relevant to hypotenuse these right triangles? At what ratio are the areas of these triangles? A smaller rectangular triangle has legs 6 and
The lengths of the corresponding sides of two rectangular triangles are in the ratio 2:5. At what ratio are medians relevant to hypotenuse these right triangles? At what ratio are the areas of these triangles? A smaller rectangular triangle has legs 6 and - Rectangle vs square
 One side of the rectangle is 1 cm shorter than the side of the square. The second side is 3 cm longer than the side of the square. The square and rectangle have the same area. Calculate the length of the sides of a square and a rectangle.
One side of the rectangle is 1 cm shorter than the side of the square. The second side is 3 cm longer than the side of the square. The square and rectangle have the same area. Calculate the length of the sides of a square and a rectangle. - Two conductors
 Two conductors have resistance Rs=5 ohms when connected in series and Rp=1.2 ohms when connected in parallel. Calculate the value of the resistors.
Two conductors have resistance Rs=5 ohms when connected in series and Rp=1.2 ohms when connected in parallel. Calculate the value of the resistors. - Garage
 There are two laths in the garage opposite one another: one 2 meters long and the second 3 meters long. They fall against each other and stay against the opposite walls of the garage. Both laths cross 70 cm above the garage floor. How wide is the garage?
There are two laths in the garage opposite one another: one 2 meters long and the second 3 meters long. They fall against each other and stay against the opposite walls of the garage. Both laths cross 70 cm above the garage floor. How wide is the garage? - Similarity coefficient
 Given triangle ABC with sides a = 12 cm b = 9 cm c = 7 cm and triangle DEF with sides d = 8.4 cm, e = 6.3 cm f = 4.9 cm Find out if triangles ABC and DEF are similar if so, write the similarity coefficient and according to which sentence they are similar
Given triangle ABC with sides a = 12 cm b = 9 cm c = 7 cm and triangle DEF with sides d = 8.4 cm, e = 6.3 cm f = 4.9 cm Find out if triangles ABC and DEF are similar if so, write the similarity coefficient and according to which sentence they are similar - An electrician 3
 In setting up a wiring job, an electrician ran the following lengths of wire: 340 m, 203 m, 74 m, and 99 m. Find the total length of wire used.
In setting up a wiring job, an electrician ran the following lengths of wire: 340 m, 203 m, 74 m, and 99 m. Find the total length of wire used. - Clock Tower
 What angle is between the hands-on Clock Tower when it shows 17 hours and 35 minutes?
What angle is between the hands-on Clock Tower when it shows 17 hours and 35 minutes? - Chimney and tree
 Calculate the height of the factory chimney, which casts a shadow of 6.5 m long in the afternoon. At the same time, a 6 m high tree standing near it casts a shadow 25 dm long.
Calculate the height of the factory chimney, which casts a shadow of 6.5 m long in the afternoon. At the same time, a 6 m high tree standing near it casts a shadow 25 dm long. - Distances 79974
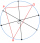 The picture shows three villages, A, B, and C, and their mutual air distances. The new straight railway line is to be built so that all the villages are the same distance from the line and that this distance is the smallest possible. How far will they be
The picture shows three villages, A, B, and C, and their mutual air distances. The new straight railway line is to be built so that all the villages are the same distance from the line and that this distance is the smallest possible. How far will they be - Bases
 The length of the bases trapezium is in ratio 2:4. The length of the midline is 20. How long are the bases of a trapezoid?
The length of the bases trapezium is in ratio 2:4. The length of the midline is 20. How long are the bases of a trapezoid?
Do you have unsolved math question and you need help? Ask a question, and we will try to solve it. We solve math question.
