Planimetrics - math word problems - page 140 of 184
Number of problems found: 3667
- Children's room
The children's room is a square with a side of 3m. What is the area of the room layout on a 1:50 scale plan? - Right isosceles triangle
The right isosceles triangle has an altitude x drawn from the right angle to the hypotenuse, dividing it into two equal segments. One segment is 5 cm long. What is the area of the triangle? - Quadrilateral 42151
Calculations from geometry: The ratios of the sides of the quadrilateral are 3 : 6:4.5 : 3.5. Calculate their lengths if the circumference is 51 cm. The sizes of the angles in the quadrilateral are equal to 29°30', 133°10', and 165°20'. What is the size o - Concerning 6294
Two isosceles triangles have the same angle at the apex concerning the base. One has a 17 cm long arm and a 10 cm long base. The second has a base length of 8 cm. Determine the length of his arm. - Shadow and light
Nine meters height poplar tree has a shadow 16.2 meters long. How long does shadow have at the same time as Joe if he is 1,4m tall? - N-gon
How many diagonals have convex 30-gon? - Different 42191
How many different triangles with vertices formed by points A, B, C, D, E, and F can we create? - The spinner
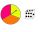The spinner below is spun 12 times. It landed on I 4 times, II 7 times, and III 1 time. What is the difference between the experimental and theoretical probabilities of landing on the II? - Dimensions and area
Determine the actual dimensions of the kitchen and its area if its dimensions on the plan with a scale of 1:200 are 3.5 cm and 4 cm. - Square garden
The square garden has an area of 36 square meters. What area will its image have in the 1:60 scale? - Inequality triangle
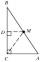The heel of height from the vertex C in the triangle ABC divides the side AB in the ratio 1:2. Prove that in the usual notation of the lengths of the sides of the triangle ABC, the inequality 3 | a-b | < c. - Construct 8
Construct an analytical geometry problem where it is asked to find the vertices of a triangle ABC: The vertices of this triangle are points A (1,7), B (-5,1) C (5, -11). The said problem should be used the concepts of distance from a point to a line, rati - Shadow
A meter pole perpendicular to the ground throws a shadow of 40 cm long. The house throws a shadow 6 meters long. What is the height of the house? - A cliff
A line from the top of a cliff to the ground passes just over the top of a pole 5 ft high. It meets the ground at a point 8 ft from the base of the pole. The point is 93 ft from the base of the cliff. How high is the cliff? - Isosceles 7566
A right isosceles triangle is inscribed in the circle with r = 8 cm. Find triangle area S. How much percent does the triangle occupy the area of the circle? - Lighthouse
Marcel (point J) lies in the grass and sees the top of the tent (point T) and, behind it, the top of the lighthouse (P). | TT '| = 1.2m, | PP '| = 36m, | JT '| = 5m. Marcel lies 15 meters away from the sea (M). Calculate the lighthouse distance from the s - Respectively 80982
The vertices of the square ABCD are joined by the broken line DEFGHB. The smaller angles at the vertices E, F, G, and H are right angles, and the line segments DE, EF, FG, GH, and HB measure 6 cm, 4 cm, 4 cm, 1 cm, and 2 cm, respectively. Determine the ar - Three altitudes
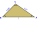A triangle with altitudes 4, 5, and 6 cm is given. Calculate the lengths of all medians and all sides in a triangle. - Bisector 2
ABC is an isosceles triangle. While AB=AC, AX is the bisector of the angle ∢BAC meeting side BC at X. Prove that X is the midpoint of BC. - Diagonal intersect
Isosceles trapezoid ABCD with length bases | AB | = 6 cm, CD | = 4 cm is divided into four triangles by the diagonals intersecting at point S. How much of the area of the trapezoid are ABS and CDS triangles?
Do you have homework that you need help solving? Ask a question, and we will try to solve it. Solving math problems.
