Right triangle practice problems - page 82 of 86
Number of problems found: 1716
- Calculate 65014
The radius of the circle is 5.5 cm. The height is 2.3 cm, which is the chord's distance. How can we calculate the length of the string? - Circle chord
Calculate the length of the chord of the circle with radius r = 10 cm, the length of which is equal to the distance from the circle's center. - Regular quadrilateral pyramid
What is the volume of a regular quadrilateral pyramid if the edge of the base is 8 cm long and the height of the side wall is 5 cm? - Fifty-meter 80722
Calculate how many hectoliters of water can fit in a fifty-meter sloped pool; if the smallest depth is 1.2 m and the largest depth is 3 m, the width of the pool is 20 m. - Chord 4
I need to calculate the circumference of a circle, and I know the chord length c=16 cm and the distance from the center d=15 cm chord to the circle. - Quadrilateral pyramid
What is the volume of a regular quadrilateral pyramid? The pyramid height is 30 cm, and the wall height is 50 cm. - Common chord
Two circles with radii 18 cm and 20 cm intersect at two points. Its common chord is long 11 cm. What is the distance of the centers of these circles? - Ellipse
Ellipse is expressed by equation 9x² + 25y² - 54x - 100y - 44 = 0. Find the length of primary and secondary axes, eccentricity, and coordinates of the ellipse's center. - Rectangular 26091
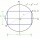The circular running track has a diameter of 130 meters. Can a rectangular surface with dimensions of 12m and 50m be grassed inside the circle? - Quadrilateral pyramid,
A quadrilateral pyramid has a rectangular base with 24 cm and 13 cm dimensions. The height of the pyramid is 18cm. Calculate 1/the area of the base 2/casing area 3/pyramid surface 4/volume of the pyramid - Calculate the chord
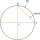The circle's radius is r=8.9 cm, and the chord AB of this circle has a length of 16 cm. Calculate the distance of chord AB from the center of the circle. - Circle chord
What is the length x of the chord circle of diameter 115 m if the distance from the center circle is 11 m? - IS trapezoid
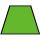Isosceles trapezoid arm measured 46 cm. Height is 38 cm, and the middle segment is 84 cm. Find the length of its bases. - Circles
In the circle with a radius, 7.5 cm is constructed of two parallel chords whose lengths are 9 cm and 12 cm. Calculate the distance of these chords (if there are two possible solutions, write both). - Calculate 3561
There is a 12 cm long chord in a circle with a radius of 10 cm. Calculate the distance of the chord from the center of the circle. - Cone 15
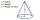The radius of the base of a right circular cone is 14 inches, and its height is 18 inches. What is the slant height? - Axial section
The diagonal of the axial section of the rotating cylinder is 6 cm, and its surface is 30 cm square. Calculate the radius of the base. - Determine
Determine which type of quadrilateral ABCD is and find its perimeter if you know the coordinates of vertices: A/2,4 /, B / -2,1 /, C / -2, -2 /, D/2, -5 /. - Chord and radius
Calculate the radius of a circle whose chord XY is 8 cm long and whose center is 3 cm from the chord. - The chord
Calculate a chord length where the distance from the circle's center (S, 24 cm) equals 16 cm.
Do you have homework that you need help solving? Ask a question, and we will try to solve it. Solving math problems.
