Solid geometry, stereometry - page 115 of 121
Number of problems found: 2404
- Through 82036
5 m³ of water flows through the pipe in 1 second at a maximum speed of 2 m/s. What is the pipe radius? - The projection
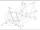In axonometry, construct the projection of a perpendicular 4-sided pyramid with a square base ABCD in the plane. The base triangle gives the axonometry. We know the center of the base S, the point of the base A, and the height of the pyramid v. - Octagonal pyramid
Draw an octagonal pyramid in free parallel projection if the length of the edge a = 3 cm and the height of the pyramid v = 6 cm. - Hectoliters 4550
The water's surface in the pool is a rectangle 50 meters long and 12 meters wide. The water depth rises evenly from 1 meter at one end of the pool to 3 meters at the other end of the pool (longer sides). Determine the amount of water in the pool in hectol - North Pole
What is the shortest distance across the globe's surface on a scale of 1:1,000,000 from the equator to the North Pole? - Freezer
The freezer has the shape of a cuboid with internal dimensions of 12 cm, 10 cm, and 30 cm. A layer of ice 23 mm thick was formed on the freezer's inner walls (and on the opening). How many liters of water will drain if we dispose of the freezer? - Ice rink
A rectangular rink measuring 15m and 20m long needs to be covered with a layer of ice 4.5cm high. How many liters of water are needed to create ice? - Distribute 32451
The king cannot decide how to distribute 4 cubes of pure gold, which have edges of length 3cm, 4cm, 5cm, and 6cm, to two sons as fairly as possible. Design a solution so that the cubes do not have to be cut. - Velocity ratio
Determine the ratio at which the fluid velocity in different parts of the pipeline (one piece has a diameter of 5 cm and the other has a diameter of 3 cm) when you know that every point of the liquid is the product of the area of the tube [S] and the flui - Dice - 5 times
We roll the dice five times. Make sentences: a) 3 events that definitely cannot happen. Write a reason for each. b) 3 events that will definitely occur; write a reason for each. Another problem: 3 events that may or may not occur for each. Write a reason. - Ice + water
A rectangular ice rink measuring 60 m by 30 m had a layer of ice 3 cm high. How many liters of water were used to create the ice? - Eiffel Tower
The Eiffel Tower in Paris is 300 meters high and made of steel. It weighs 8,000 tons. If the tower model made of the same material weighs 1.8 kg, how tall is it? - Seawater
Seawater density is 1025 kg/m³, and ice is 920 kg/m³. Eight liters of seawater froze and created a cube. Calculate the size of the cube edge. - Soap bubble
A conductive soap bubble with a radius of r=2 cm and charged to a potential of φ= 10000 V will burst into a drop of water with a radius of r1= 0.05 cm. What is the potential φ1 of the drop? - Pipes
The water pipe has a cross-section 1903 cm². An hour has passed 859 m³ of water. How much water flows through the pipe with cross-section 300 cm² per 11 hours if water flows at the same speed? - Shortest walk
An ant is crawling around this cube. The cube is made of wire. Each side of the cube is 3 inches long. (Those sides are called edges.) Points A and B are vertices of the cube. What is the least distance the ant would have to crawl if it starts from point - Scale
The student drew the cylinder in scale 7:1. How many times is the volume of the cylinder smaller in reality? - Equilateral cylinder
A sphere is inserted into the rotating equilateral cylinder (touching the bases and the shell). Prove that the cylinder has both a volume and a surface half larger than an inscribed sphere. - Octahedron - sum
On each wall of a regular octahedron is written one of the numbers 1, 2, 3, 4, 5, 6, 7, and 8, wherein on different sides are different numbers. John makes the sum of the numbers written on three adjacent walls for each wall. Thus got eight sums, which al - Perpendicular 5865
We cut the cube with two mutually perpendicular cuts, each parallel to one of the cube's walls. By what percentage is the sum of the surfaces of all cuboids created in this way greater than the surface of the original cube?
Do you have unsolved math question and you need help? Ask a question, and we will try to solve it. We solve math question.
