Solid geometry, stereometry - page 116 of 121
Number of problems found: 2409
- Shortest walk
 An ant is crawling around this cube. The cube is made of wire. Each side of the cube is 3 inches long. (Those sides are called edges.) Points A and B are vertices of the cube. What is the least distance the ant would have to crawl if it starts from point
An ant is crawling around this cube. The cube is made of wire. Each side of the cube is 3 inches long. (Those sides are called edges.) Points A and B are vertices of the cube. What is the least distance the ant would have to crawl if it starts from point - Velocity ratio
 Determine the ratio at which the fluid velocity in different parts of the pipeline (one piece has a diameter of 5 cm and the other has a diameter of 3 cm) when you know that every point of the liquid is the product of the area of the tube [S] and the flui
Determine the ratio at which the fluid velocity in different parts of the pipeline (one piece has a diameter of 5 cm and the other has a diameter of 3 cm) when you know that every point of the liquid is the product of the area of the tube [S] and the flui - Equilateral cylinder
 A sphere is inserted into the rotating equilateral cylinder (touching the bases and the shell). Prove that the cylinder has both a volume and a surface half larger than an inscribed sphere.
A sphere is inserted into the rotating equilateral cylinder (touching the bases and the shell). Prove that the cylinder has both a volume and a surface half larger than an inscribed sphere. - Octahedron - sum
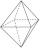 On each wall of a regular octahedron is written one of the numbers 1, 2, 3, 4, 5, 6, 7, and 8, wherein on different sides are different numbers. John makes the sum of the numbers written on three adjacent walls for each wall. Thus got eight sums, which al
On each wall of a regular octahedron is written one of the numbers 1, 2, 3, 4, 5, 6, 7, and 8, wherein on different sides are different numbers. John makes the sum of the numbers written on three adjacent walls for each wall. Thus got eight sums, which al - Perpendicular 5865
 We cut the cube with two mutually perpendicular cuts, each parallel to one of the cube's walls. By what percentage is the sum of the surfaces of all cuboids created in this way greater than the surface of the original cube?
We cut the cube with two mutually perpendicular cuts, each parallel to one of the cube's walls. By what percentage is the sum of the surfaces of all cuboids created in this way greater than the surface of the original cube? - Sphere floating
 Will a hollow iron ball float with an outer diameter of d1 = 20cm and an inside diameter of d2 = 19cm in the water? The iron density is 7.8 g/cm³. (Instructions: Calculate the average sphere density and compare it with the water density. )
Will a hollow iron ball float with an outer diameter of d1 = 20cm and an inside diameter of d2 = 19cm in the water? The iron density is 7.8 g/cm³. (Instructions: Calculate the average sphere density and compare it with the water density. ) - Cuboids
 Two separate cuboids with different orientations are in space. Determine the angle between them, knowing the direction cosine matrix for each separate cuboid. u1=(0.62955056, 0.094432584, 0.77119944) u2=(0.14484653, 0.9208101, 0.36211633)
Two separate cuboids with different orientations are in space. Determine the angle between them, knowing the direction cosine matrix for each separate cuboid. u1=(0.62955056, 0.094432584, 0.77119944) u2=(0.14484653, 0.9208101, 0.36211633) - Float boya
 A 0.5-meter spherical float is a location mark for a fishing boat anchor. It floats in salt water. Find the depth to which the float sinks if the material of which the float is made weighs 8 kilograms per cubic meter and saltwater weighs 1027 kg/m³.
A 0.5-meter spherical float is a location mark for a fishing boat anchor. It floats in salt water. Find the depth to which the float sinks if the material of which the float is made weighs 8 kilograms per cubic meter and saltwater weighs 1027 kg/m³. - Water channel
 The cross-section of the water channel is a trapezoid. The bottom width is 19.7 m, the water surface width is 28.5 m, and the side walls have a slope of 67°30' and 61°15'. Calculate how much water flows through the channel in 5 minutes if the water flows
The cross-section of the water channel is a trapezoid. The bottom width is 19.7 m, the water surface width is 28.5 m, and the side walls have a slope of 67°30' and 61°15'. Calculate how much water flows through the channel in 5 minutes if the water flows - Paper box
 Calculate the paper consumption on the box-shaped quadrangular prism with rhombic footstall, base edge a=6 cm, and the adjacent base edges form an angle alpha = 60 °. The box height is 10 cm. How much m² of the paper is consumed 100 such boxes?
Calculate the paper consumption on the box-shaped quadrangular prism with rhombic footstall, base edge a=6 cm, and the adjacent base edges form an angle alpha = 60 °. The box height is 10 cm. How much m² of the paper is consumed 100 such boxes? - Flowerbed
 The flowerbed has the shape of a truncated pyramid. The bottom edge of the base a = 10 m, and the upper base b = 9 m. The deviation angle between the edge and the base is alpha = 45°. What volume is needed to make this flowerbed? How many plants can be pl
The flowerbed has the shape of a truncated pyramid. The bottom edge of the base a = 10 m, and the upper base b = 9 m. The deviation angle between the edge and the base is alpha = 45°. What volume is needed to make this flowerbed? How many plants can be pl - Eight blocks
 Dana had the task of saving the eight blocks of these rules: 1. Between two red cubes must be a different color. 2. Between two blue must be two different colors. 3. Between two green must be three different colors. 4. Between two yellow blocks must be fo
Dana had the task of saving the eight blocks of these rules: 1. Between two red cubes must be a different color. 2. Between two blue must be two different colors. 3. Between two green must be three different colors. 4. Between two yellow blocks must be fo - Circular pool
 The pool's base is a circle with a radius r = 10 m, excluding a circular segment that determines the chord length of 10 meters. The pool depth is h = 2m. How many hectoliters of water can fit into the pool?
The pool's base is a circle with a radius r = 10 m, excluding a circular segment that determines the chord length of 10 meters. The pool depth is h = 2m. How many hectoliters of water can fit into the pool? - Tetrahedral pyramid 8
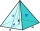 Let all the side edges of the tetrahedral pyramid ABCDV be equally long and its base let us be a rectangle. Find its volume if you know the deviations A=52° B=56° between the planes of adjacent sidewalls and the base plane. The height of the pyramid is h=
Let all the side edges of the tetrahedral pyramid ABCDV be equally long and its base let us be a rectangle. Find its volume if you know the deviations A=52° B=56° between the planes of adjacent sidewalls and the base plane. The height of the pyramid is h= - Quadrilateral oblique prism
 What is the volume of a quadrilateral oblique prism with base edges of length a = 1m, b = 1.1m, c = 1.2m, d = 0.7m if a side edge of length h = 3.9m has a deviation from the base of 20° 35' and the edges a, b form an angle of 50.5°?
What is the volume of a quadrilateral oblique prism with base edges of length a = 1m, b = 1.1m, c = 1.2m, d = 0.7m if a side edge of length h = 3.9m has a deviation from the base of 20° 35' and the edges a, b form an angle of 50.5°? - Base RR odd
 The base of the prism is an isosceles trapezoid ABCD with bases AB = 12 cm, and CD = 9 cm. The angle at vertex B is 48° 10'. Determine the volume and area of the prism if its height is 35 cm.
The base of the prism is an isosceles trapezoid ABCD with bases AB = 12 cm, and CD = 9 cm. The angle at vertex B is 48° 10'. Determine the volume and area of the prism if its height is 35 cm. - Side wall planes
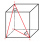 Find the volume and surface of a cuboid whose side c is 30 cm long and whose body diagonal forms angles of 24°20' and 45°30' with the planes of the side walls.
Find the volume and surface of a cuboid whose side c is 30 cm long and whose body diagonal forms angles of 24°20' and 45°30' with the planes of the side walls. - The spacecraft
 The spacecraft spotted a radar device at an altitude angle alpha = 34 degrees 37 minutes and had a distance of u = 615km from Earth's observation point. Calculate the distance d of the spacecraft from Earth at the moment of observation. Earth is considere
The spacecraft spotted a radar device at an altitude angle alpha = 34 degrees 37 minutes and had a distance of u = 615km from Earth's observation point. Calculate the distance d of the spacecraft from Earth at the moment of observation. Earth is considere - Cross-section of a roof
 The owner must cover the carport with a hipped roof with a rectangular cross-section of 8 m x 5 m. All roof surfaces have the same slope of 30°. Determine the price and weight of the roof if 1 m² cost €270 and weighs 43 kg.
The owner must cover the carport with a hipped roof with a rectangular cross-section of 8 m x 5 m. All roof surfaces have the same slope of 30°. Determine the price and weight of the roof if 1 m² cost €270 and weighs 43 kg. - An Elizabethan collar
 An Elizabethan collar is used to prevent an animal from irritating a wound. The angle between the opening (diameter 6 inches) with a 16-inch diameter and the side of the collar is 53 degrees. Find the surface area of the collar shown.
An Elizabethan collar is used to prevent an animal from irritating a wound. The angle between the opening (diameter 6 inches) with a 16-inch diameter and the side of the collar is 53 degrees. Find the surface area of the collar shown.
Do you have homework that you need help solving? Ask a question, and we will try to solve it. Solving math problems.
