Na obrázku 3
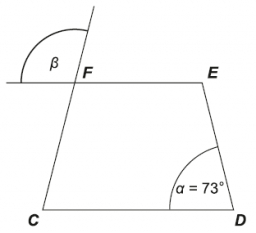
Na obrázku je znázornený rovnoramenný lichobežník CDEF. Vel’kost’ uhla α je 73 stupňov. Vypočítajte v stupňoch veľkost’ uhla β.
Vaša odpoveď:
Vaša odpoveď:
Na vyriešenie tejto úlohy sú potrebné tieto znalosti z matematiky:
Odporúčame k tejto úlohe z matematiky si pozrieť toto výukové video: video1
Súvisiace a podobné príklady:
- Rovnoramenný RRT
Rovnoramenný trojuholník má veľkosť uhlov pri základni alfa = beta = 34 stupňov 34 minút. Vypočítajte v stupňoch a minútach veľkosť uhla pri zostávajúcom vrchole trojuholníka. - Stoosemdesiat stupňov
Trojuholník má vnútorné uhly 58º 20' a 83º 40'. Vypočítajte v stupňoch veľkosť tretieho uhla . - Rovnoramenný lichobežník
Lichobežník FNGU (FN||GU) je rovnoramenný. Veľkosť uhla pri vrchole N je 63 stupňov. Vypočítajte veľkosť uhla pri vrchole U. - Trojuholník - PT - uhol
V pravouhlom trojuholníku je veľkosť uhla 40°. Nájdite veľkosť ostatných uhlov trojuholníka v stupňoch. - Súčet 11
Súčet dvoch uhlov je 89°. Jeden uhol má veľkosť 64°. Aká je veľkosť druhého uhla v stupňoch? - Rovnoramenný 42
Rovnoramenný trojuholník má veľkosť uhla pri základni 78° 20'. Vypočítajte veľkosť uhla medzi ramenami. - V rovnobežníku 3
V rovnobežníku ABCD platí AB = 8, BC = 5, BD = 7 . Vypočítajte veľkosť uhla α = ∠DAB (v stupňoch).
