Pytagorova veta - slovné úlohy a príklady - strana 48 z 72
Počet nájdených príkladov: 1429
- Rotačného 28501
Do ktorého z vrecúšok v tvare plášťa rotačného kužeľa sa zmestí väčšie množstvo praženej kukurice? Prvé vrecko má výšku 20 cm a dĺžka jeho strany je 24 cm, druhé vrecko má polomer podstavy 10 cm a výšku 25 cm. - Stĺp
Vypočítajte objem a povrch podporného stĺpu tvare kolmého štvorbokého hranola, ktorého podstavou je kosoštvorec s uhlopriečku u1 = 102cm, u2 = 64cm. Výška stĺpa je 1,5m. - Objem 40
Objem kvádra so štvorcovou podstavovou je 64 cm³ a odchýlka telesovej uhlopriečky od roviny podstavy je 45 stupňov. Vypočítajte jeho povrch. - Štvorboký ihlan
Kôlňa tvaru kvádra je krytá strechou tvaru štvorbokého ihlana s podstavou o hranách 6m a 3m a výškou 2,5 m. Koľko m² (metrov štvorcových) je potrebné zakúpiť, ak na prekrytie krytiny a odpad sa počíta 40% navyše?
- Zrezaný ihlan 2
Vypočítajte objem pravidelného šesťbokého zrezaného ihlana, ak je dĺžka hrany dolnej podstavy 30 cm, hornej podstavy 12 cm a ak dĺžka bočnej hrany je 41 cm. - Cukrárskej 7318
Cukrárka potrebuje z cukrárskej hmoty v tvare gule o polomere 25cm vyrezať ozdobu v tvare kužeľa. Určte polomer podstavy ozdoby a (a výšku h) tak, aby sa na výrobu ozdoby použilo čo najviac hmoty. - Obvod 58
Obvod štvobokého ihlava je 48 m a jeho výška ja 2,5m; koľko bude stáť plech na tento ihlan, keď 1m² stojí 1,5€; do plochy sa počíta aj 12% strata na spoje a záhyby. - Súčiastka
Súčiastka tvaru zrezaného kúžeľa s polomermi podstáv 4 cm a 22 cm sa má pretaviť na súčiastku tvaru valca rovnakej výšky ako pôvodná súčiastka. Aký polomer podstavy bude mať nová súčiastka? - Stan 8
Stan tvaru ihlana má podstavu štvoreca s veľkosťou strany 2,2m a výšku 1,8m. Koľko metrov štvorcových stanového plátna je treba na jeho zhotovenie ak počítame päť percent naviac na založenie?
- Guľa vs. kocka
Koľko % povrchu gule s polomerom 12 cm tvorí povrch kocky vpísanej robiť teto gule? - Terwilliker 75264
Hromada soli bola uložená v tvare kužeľa. Pán Terwilliker vie, že hromada je 20 stôp vysoká a 102 stôp v obvode na základni. Aká plocha kónickej plachty (veľký kus materiálu) je potrebná na zakrytie hromady? - Pravidelného 15613
Vežička má tvar pravidelného štvorbokého ihlana s podstavnou hranou dĺžky 0,8 m. Výška vežičky je 1,2 m. Koľko metrov štvorcových je potrebných na jej pokrytie, ak počítame na odpad 10% plechu navyše. - Vrchol veže Vrchol veže má tvar pravidelného šesťbokého ihlanu. Podstavná hrana má dĺžku 1,2 m, výška ihlanu je 1,6 m. Koľko metrov štvorcových plechu je potreba na pokrytie vrchole veže, ak je na spoje, prekrytie a odpad potrebná 15% plechu naviac?
- Štvorboký ihlan
Koľko metrov štvorcových je potreba na pokrytie veže tvaru pravidelného štvorbokého ihlanu o podstavnej hrane 10 metrov, ak je odchýlka bočnej hrany od roviny podstavy 68°? Pri pokrytí sa počíta s odpadom 10%.
- Sily
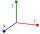Na bod I pôsobia tri navzájom kolmé sily F1=6 N, F2=15 N, F3=20 N. Určte výslednicu F a uhly, ktoré zviera výslednica so zložkami F1, F2, F3. - Štvorcových 23801
Správca hradu sa pokúša odhadnúť, koľko štvorcových metrov plechu bude približne treba na novú strechu veže. Strecha má tvar kužeľa. Správca hradu vie, že priemer veže je 4,6 metra a výška je 5,2 metra. Koľko štvorcových metrov strecha meria? - Rovnostranný ihlan Ťažítko zo skla má tvar pravidelného štvorbokého ihlana o hrane podstavy 10cm. Steny plášťa sú rovnostranné trojuholníky. Akú hmotnosť v gramoch má ťažítko, ak hustota skla je 2500kg/m³?
- Matematika 2
Do prepravného kontajnera s rozmermi a=10 m, b=4m, c=3m bola umiestnená drevená debna s rozmermi d=3m, e=4m a f=3m. Aká je maximálna dĺžka rovnej neohybnej tyče so zanedbateľným priemerom, ktorú je možné v tejto situácii ešte do kontejnera umiestniť? - Strecha 16
Strecha veže má tvar pravidelného 4-bokeho ihlana a výškou 4m a hranou podstavy 6m. Zistilo sa že je poškodených 25% krytiny na streche. Koľko metrov štvorcových krytiny treba na opravu strechy?
Vypočítajte hmotnosť dreveného pravidelného trojbokého hranola s výškou rovnajúcou sa obvodu podstavy a postavou vpísanou do kružnice s polomerom 6, M cm, kde M je mesiac vášho narodenia. Hustota duba je 680 kg/m³.Máš úlohu, nad ktorou si lámeš aspoň 10 minút hlavu? Pošli nám úlohu a my Ti ju skúsime vypočítať. Riešenie príkladov z matematiky.
