Príklady pre stredoškolákov - strana 33 z 225
Počet nájdených príkladov: 4484
- Vo vrecúšku 5
 Vo vrecúšku je 5 čokoládových, 3 tvarohové a 2 marhuľové croissanty. Croissanty vyberáme náhodne v vrecúška. Aká je pravdepodobnosť, že vytiahneme 1 čokoládový, 1 tvarohový a 1 marhuľový croissant bez vrátenia?
Vo vrecúšku je 5 čokoládových, 3 tvarohové a 2 marhuľové croissanty. Croissanty vyberáme náhodne v vrecúška. Aká je pravdepodobnosť, že vytiahneme 1 čokoládový, 1 tvarohový a 1 marhuľový croissant bez vrátenia? - Obvod 51
 Obvod trojuholníka ABC je 162 dm. Dĺžky jeho strán sú v pomeroch a: b = 2:3 a a : c = 8:7. Urč dĺžky strán trojuholníka.
Obvod trojuholníka ABC je 162 dm. Dĺžky jeho strán sú v pomeroch a: b = 2:3 a a : c = 8:7. Urč dĺžky strán trojuholníka. - Zo štvorca 2
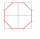 Zo štvorca o strane 4 cm odrežeme štyri pravouhlé rovnoramenné trojuholníky s pravým uhlom vo vrcholoch štvorca a s preponou √2 cm. Dostaneme osemuholník. Vypočítajte jeho obvod, ak plocha osemuholníka je 14cm².
Zo štvorca o strane 4 cm odrežeme štyri pravouhlé rovnoramenné trojuholníky s pravým uhlom vo vrcholoch štvorca a s preponou √2 cm. Dostaneme osemuholník. Vypočítajte jeho obvod, ak plocha osemuholníka je 14cm². - Odvesny 6
 Odvesny pravouhlého trojuholníka majú dĺžky 30 cm a 40 cm. Akú veľkosť má výška zostrojená na preponu trojuholníka?
Odvesny pravouhlého trojuholníka majú dĺžky 30 cm a 40 cm. Akú veľkosť má výška zostrojená na preponu trojuholníka? - Prúd vodičom
 Určite prúd prechádzajúci vodičom, ak za jednu minútu prešiel jeho prierezom náboj 150 C.
Určite prúd prechádzajúci vodičom, ak za jednu minútu prešiel jeho prierezom náboj 150 C. - Čas prechodu náboja
 Za akú dobu prejde pri prúde 1 A vodičom náboj 600 C?
Za akú dobu prejde pri prúde 1 A vodičom náboj 600 C? - Keby Petra
 Keby Petra čítala denne o 4 strany viac, prečítala by knihu o 2 dni skôr, ako keby čítala denne 6 strán. Koľko strán má kniha?
Keby Petra čítala denne o 4 strany viac, prečítala by knihu o 2 dni skôr, ako keby čítala denne 6 strán. Koľko strán má kniha? - Rovnoramenný 43
 Rovnoramenný lichobežník ABCD má obsah 36 cm². Jedna jeho základňa je 2-krát dlhšia ako druhá. Výška je 4 cm. Vypočítaj obvod lichobežníka.
Rovnoramenný lichobežník ABCD má obsah 36 cm². Jedna jeho základňa je 2-krát dlhšia ako druhá. Výška je 4 cm. Vypočítaj obvod lichobežníka. - Číslo 40
 Číslo 6 rozdeľte na tri sčítance x, y, z tak, aby x : y = 4 : 3, y : z = 1 : 2.
Číslo 6 rozdeľte na tri sčítance x, y, z tak, aby x : y = 4 : 3, y : z = 1 : 2. - Úroky - sporenie
 Koľko musím mesačne sporiť, aby som za 5 rokov nasporil 100 000 Sk, ak je úroková miera 4 %, úrokovacie obdobie jeden mesiac a daň z úrokov 15 %?
Koľko musím mesačne sporiť, aby som za 5 rokov nasporil 100 000 Sk, ak je úroková miera 4 %, úrokovacie obdobie jeden mesiac a daň z úrokov 15 %? - Kameň 4
 Kameň bol vrhnutý zvisle nahor rýchlosťou vo= 15 m/s. Za akú dobu bude vo výške a) 10 m, b)12 m?
Kameň bol vrhnutý zvisle nahor rýchlosťou vo= 15 m/s. Za akú dobu bude vo výške a) 10 m, b)12 m? - V rovnobežníku 3
 V rovnobežníku ABCD platí AB = 8, BC = 5, BD = 7 . Vypočítajte veľkosť uhla α = ∠DAB (v stupňoch).
V rovnobežníku ABCD platí AB = 8, BC = 5, BD = 7 . Vypočítajte veľkosť uhla α = ∠DAB (v stupňoch). - Vydatá
 V izbe je šesť manželských párov. Ak sa náhodne vyberú dvaja ľudia. Nájdite pravdepodobnosť, že; a) sú manželia. b) jeden je muž a jeden žena.
V izbe je šesť manželských párov. Ak sa náhodne vyberú dvaja ľudia. Nájdite pravdepodobnosť, že; a) sú manželia. b) jeden je muž a jeden žena. - Investícia výnos
 Ak investor investuje 2 000 USD 1. januára, každý rok sa mu garantuje výnos 4 % ročne. Ak sa úroky počítajú 31. decembra, koľko bude účet na konci 10. roku?
Ak investor investuje 2 000 USD 1. januára, každý rok sa mu garantuje výnos 4 % ročne. Ak sa úroky počítajú 31. decembra, koľko bude účet na konci 10. roku? - Štyria 10
 Štyria chlapci si rozdelili výhru 680 € v pomere 2 : 4:1:3. Koľko eur dostal chlapec, ktorého podiel na výhre bol najväčší?
Štyria chlapci si rozdelili výhru 680 € v pomere 2 : 4:1:3. Koľko eur dostal chlapec, ktorého podiel na výhre bol najväčší? - Obvod 50
 Obvod trojuholníka je 125 cm. Najkratšia strana je o 12 cm kratšia ako najdlhšia strana. Najdlhšia strana je o 7 cm dlhšia ako stredná strana. Aká dlhá je stredná strana?
Obvod trojuholníka je 125 cm. Najkratšia strana je o 12 cm kratšia ako najdlhšia strana. Najdlhšia strana je o 7 cm dlhšia ako stredná strana. Aká dlhá je stredná strana? - Jarka 2
 Jarka dostala v priebehu dňa tri rôzne známky (1-5). Koľko je možností pre známky, ktoré mohla dostať? A) 6 B) 8 C) 10 D) 12
Jarka dostala v priebehu dňa tri rôzne známky (1-5). Koľko je možností pre známky, ktoré mohla dostať? A) 6 B) 8 C) 10 D) 12 - Hmotnosť žalúdka
 Hmotnosti žalúdka sú normálne rozdelené, s priemerom 1314 g a štandardnou odchýlkou 113 g. Uveďte pravdepodobnosť, že náhodne vybraný žalúdok váži viac ako 1118 g. (Vypočítajte pravdepodobnosti s použitím aspoň 4 desatinných miest. )
Hmotnosti žalúdka sú normálne rozdelené, s priemerom 1314 g a štandardnou odchýlkou 113 g. Uveďte pravdepodobnosť, že náhodne vybraný žalúdok váži viac ako 1118 g. (Vypočítajte pravdepodobnosti s použitím aspoň 4 desatinných miest. ) - Všetky násobky
 Množina A je množina všetkých násobkov 2 a množina B je množina všetkých násobkov 3. Ak P (A) = 0,6 a P (B) = 0,3. Nájdite P (AUB).
Množina A je množina všetkých násobkov 2 a množina B je množina všetkých násobkov 3. Ak P (A) = 0,6 a P (B) = 0,3. Nájdite P (AUB). - Banka 5
 Banka ponúka termínovaný učet s možnosťou predčasného výberu s úrokovou mierou 1,85 percent pa (pa= per annum = ročne). Milan naň vložil 2. januára 2 500 eur. Koľko eur získa, ak peniaze vyberie po 8 mesiacoch?
Banka ponúka termínovaný učet s možnosťou predčasného výberu s úrokovou mierou 1,85 percent pa (pa= per annum = ročne). Milan naň vložil 2. januára 2 500 eur. Koľko eur získa, ak peniaze vyberie po 8 mesiacoch?
Máš príklad, ktorý si tu nenašiel vyriešenú? Pošli nám príklad a my Ti ho skúsime vypočítať.
