Príklady pre stredoškolákov - strana 3 z 225
Počet nájdených príkladov: 4484
- Jednotková kružnica
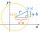 V karteziánskej súradnicovej sústave je daná jednotková kružnica, na ktorej ležia body A a B. Bod O je počiatok a má súradnice (0,0) a bod B súradnice (1,0). Veľkosť uhla BOA je 151°. Určte x-ovú súradnicu bodu A.
V karteziánskej súradnicovej sústave je daná jednotková kružnica, na ktorej ležia body A a B. Bod O je počiatok a má súradnice (0,0) a bod B súradnice (1,0). Veľkosť uhla BOA je 151°. Určte x-ovú súradnicu bodu A. - Odmeny - súťaž
 Na odmeny pre troch najlepších súťažiacich bola pripravená finančná čiastka v korunách. Prvý súťažiaci získal polovicu tejto sumy. Druhý súťažiaci dostal 300 korún. Tretí súťažiaci získal zvyšok pripravenej čiastky, čo bolo trikrát menej korún, než získal
Na odmeny pre troch najlepších súťažiacich bola pripravená finančná čiastka v korunách. Prvý súťažiaci získal polovicu tejto sumy. Druhý súťažiaci dostal 300 korún. Tretí súťažiaci získal zvyšok pripravenej čiastky, čo bolo trikrát menej korún, než získal - Intenzita RTG
 Intenzita rongenového žiarenia sa zníži na polovicu pri prechode vrstvou olova s hrúbkou 13,5 mm. Určte hrúbku olovenej dosky, ktorá zoslabí intenzitu žiarenia na desatinu pôvodnej hodnoty. Ak vieme, že intenzita klesa exponenciálne.
Intenzita rongenového žiarenia sa zníži na polovicu pri prechode vrstvou olova s hrúbkou 13,5 mm. Určte hrúbku olovenej dosky, ktorá zoslabí intenzitu žiarenia na desatinu pôvodnej hodnoty. Ak vieme, že intenzita klesa exponenciálne. - Rovnica - celá čísla
 Rieš rovnicu s neznámou x z odboru prirodzených čísel 1+6+11+16+. ... ..+x=970
Rieš rovnicu s neznámou x z odboru prirodzených čísel 1+6+11+16+. ... ..+x=970 - Rady kresiel
 V prvom rade je 15 kresiel. V každom ďalšom rade je o 3 kreslá viac. Koľko kresiel celkom je v prvých 20 radoch?
V prvom rade je 15 kresiel. V každom ďalšom rade je o 3 kreslá viac. Koľko kresiel celkom je v prvých 20 radoch? - Haliere a rožky
 Za sto korún musím kúpiť sto kusov pečiva pri cenách rožok 0,50 koruny, chlieb 10 korún a žemľa 3 koruny. Koľko čoho nakúpim? (Slovenská koruna bola platidlom na Slovensku pred eurom, alebo česká koruna v Česku)
Za sto korún musím kúpiť sto kusov pečiva pri cenách rožok 0,50 koruny, chlieb 10 korún a žemľa 3 koruny. Koľko čoho nakúpim? (Slovenská koruna bola platidlom na Slovensku pred eurom, alebo česká koruna v Česku) - Futbalový turnaj
 Na futbalovom turnaji ôsmich tímov, kde hral každý s každým práve raz, boli body udeľované takto: víťaz zápasu získal 3 body, porazený 0 bodov a pri remíze si každý tím pripísal 1 bod. Na konci turnaja bol súčet bodov získaných všetkými tímami rovný 61. K
Na futbalovom turnaji ôsmich tímov, kde hral každý s každým práve raz, boli body udeľované takto: víťaz zápasu získal 3 body, porazený 0 bodov a pri remíze si každý tím pripísal 1 bod. Na konci turnaja bol súčet bodov získaných všetkými tímami rovný 61. K - Dopravné nehody
 Z celkového počtu dopravných nehôd sa 80% stane v obci a 20% mimo obce. Keby sa podarilo znížiť počet dopravných nehôd v obci o 40%, o koľko percent by klesol celkový počet dopravných nehôd?
Z celkového počtu dopravných nehôd sa 80% stane v obci a 20% mimo obce. Keby sa podarilo znížiť počet dopravných nehôd v obci o 40%, o koľko percent by klesol celkový počet dopravných nehôd? - Prietokový kotol
 Do prietokového ohrievača voda priteká a súčasne je z neho odvádzaná. Keby voda iba pritekala, naplnil by sa prázdny ohrievač za 18 minút. Keby voda iba odtekala, vyprázdnil by sa plný ohrievač za 20 minút. Za koľko hodín sa naplní prázdny ohrievač, ak sa
Do prietokového ohrievača voda priteká a súčasne je z neho odvádzaná. Keby voda iba pritekala, naplnil by sa prázdny ohrievač za 18 minút. Keby voda iba odtekala, vyprázdnil by sa plný ohrievač za 20 minút. Za koľko hodín sa naplní prázdny ohrievač, ak sa - Súčin 22
 Súčin troch prirodzenych cisel je 600. Keby sme jedneho činitela zmenšili o 10, zmenšil by sa súčin o 400. Keby sme namiesto toho jedneho činiteľa zväčšili o 5, zväčšil by sa súčin na dvojnásobok pôvodnej hodnoty. Ktoré tri čísla majú túto vlasnosť?
Súčin troch prirodzenych cisel je 600. Keby sme jedneho činitela zmenšili o 10, zmenšil by sa súčin o 400. Keby sme namiesto toho jedneho činiteľa zväčšili o 5, zväčšil by sa súčin na dvojnásobok pôvodnej hodnoty. Ktoré tri čísla majú túto vlasnosť? - Vlak - rozbeh
 Vlak hmotnosti 1200 ton má pri rozbiehaní dosiahnuť za 45 s rýchlosť 15 m/s. Určte jeho zrýchlenie a veľkosť sily, ktorú musí vyvinúť, ak trecia sila predstavuje 0,005 tiažovej sily vlaku.
Vlak hmotnosti 1200 ton má pri rozbiehaní dosiahnuť za 45 s rýchlosť 15 m/s. Určte jeho zrýchlenie a veľkosť sily, ktorú musí vyvinúť, ak trecia sila predstavuje 0,005 tiažovej sily vlaku. - Zrýchlenie na dráhe
 Auto zväčšilo na dráhe 54m svoju rýchlosť z 21,6 km/h na 108 km/h. Určite jeho zrýchlenie za predpokladu, že sa jedná o pohyb rovnomerne zrýchlený.
Auto zväčšilo na dráhe 54m svoju rýchlosť z 21,6 km/h na 108 km/h. Určite jeho zrýchlenie za predpokladu, že sa jedná o pohyb rovnomerne zrýchlený. - Zmes čajov-kávy
 Predavač pripravil 25 kg zmesi v cene 264 CZK za 1 kg. Prvý druh bol za 180 CZK za 1 kg a druhý za 390 CZK za kg. Koľko každého potreboval?
Predavač pripravil 25 kg zmesi v cene 264 CZK za 1 kg. Prvý druh bol za 180 CZK za 1 kg a druhý za 390 CZK za kg. Koľko každého potreboval? - Zelené karty
 Z 32 kariet vytiahneme 4 karty. Koľkými spôsobmi môžeme takto vytiahnuť a) práve 2 esá, b) 3 zelené
Z 32 kariet vytiahneme 4 karty. Koľkými spôsobmi môžeme takto vytiahnuť a) práve 2 esá, b) 3 zelené - V zásielke
 V zásielke je 40 výrobkov. Z nich sú 4 chybné. Koľkými spôsobmi môžeme vybrať 5 výrobkov tak, aby medzi nimi boli práve 3 dobré?
V zásielke je 40 výrobkov. Z nich sú 4 chybné. Koľkými spôsobmi môžeme vybrať 5 výrobkov tak, aby medzi nimi boli práve 3 dobré? - Kuchynský riad
 Dve dielne mali spoločne vyrobiť 4000 sád kuchynského riadu. Po splnení tejto úlohy sa zistilo, že prvá dielňa vyrobila o 534 sád viac, než pre ňu bolo pôvodne stanovené, druhá dielňa svoju úlohu splnila na 80 %. Koľko súprav riadu vyrobili jednotlivé die
Dve dielne mali spoločne vyrobiť 4000 sád kuchynského riadu. Po splnení tejto úlohy sa zistilo, že prvá dielňa vyrobila o 534 sád viac, než pre ňu bolo pôvodne stanovené, druhá dielňa svoju úlohu splnila na 80 %. Koľko súprav riadu vyrobili jednotlivé die - Šmykové trenie
 Akou vel'kou silou musíme pôsobit na debnu s hmotnostou 300 kg, aby sme ju mohli rovnomerným pohybom posúvat po vodorovnej podlahe, ak súcinitel' šmykového trenia medzi porchom debny a podlahy je 0,5?
Akou vel'kou silou musíme pôsobit na debnu s hmotnostou 300 kg, aby sme ju mohli rovnomerným pohybom posúvat po vodorovnej podlahe, ak súcinitel' šmykového trenia medzi porchom debny a podlahy je 0,5? - Hokej - hra
 Hokejový brankár má úspešnosť zákrokov 93,5 %. Aká je pravdepodobnosť, že v zápase, keď čelí 25 strelám, vychytá čisté konto? Aká je pravdepodobnosť, že pustí maximálne 2 góly?
Hokejový brankár má úspešnosť zákrokov 93,5 %. Aká je pravdepodobnosť, že v zápase, keď čelí 25 strelám, vychytá čisté konto? Aká je pravdepodobnosť, že pustí maximálne 2 góly? - Jurko - Ďurko
 Juraj si myslí štvorciferné číslo, o ktorom nám povedal: (a) Jeho ciferný súčet je stotina z čísla, ktoré dostanem zaokrúhlením mysleného čísla na stovky. (b) Jeho posledná číslica je o 1 väčšia ako predposledná. (c) Súčet jeho posledných dvoch číslic sa
Juraj si myslí štvorciferné číslo, o ktorom nám povedal: (a) Jeho ciferný súčet je stotina z čísla, ktoré dostanem zaokrúhlením mysleného čísla na stovky. (b) Jeho posledná číslica je o 1 väčšia ako predposledná. (c) Súčet jeho posledných dvoch číslic sa - Maturitný - RR - základňa
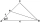 V rovnoramennom trojuholníku ABC so základňou AB platí ∠BAC = 20°, AB = 4. Os vnútorného uhla pri vrchole B pretína stranu AC v bode P. Vypočítajte dĺžku úsečky AP. Výsledok uveďte s presnosťou na dve desatinné miesta.
V rovnoramennom trojuholníku ABC so základňou AB platí ∠BAC = 20°, AB = 4. Os vnútorného uhla pri vrchole B pretína stranu AC v bode P. Vypočítajte dĺžku úsečky AP. Výsledok uveďte s presnosťou na dve desatinné miesta.
Máš príklad, ktorý si tu nenašiel vyriešenú? Pošli nám príklad a my Ti ho skúsime vypočítať.
