Tangens - slovné úlohy a príklady - strana 14 z 15
Počet nájdených príkladov: 286
- Goniometrické funkcie
Pre pravouhlý trojuholník plati: tg α= frac(7) 8 Určite hodnoty s, k aby platilo: sin α= (s)/(√ 113) cos α= (k)/(√ 113) - Remeň
Vypočítajte dĺžku remeňa na remeniciach s priemermi 105 mm a 393 mm pri vzdialenosti hriadeľov 697 mm. - Kostolná veža
Kostolnú vežu vidíme z cesty pod uhlom 52°. Keď sa vzdialime o 29 metrov, je ju vidieť pod uhlom 21°. Aká je vysoká? - Pohár s džúsom
Pohár tvaru valca výšky 18 cm a priemeru podstavy 8 cm je naplnený džusom tak že hladina je 4 cm pod okrajom pohára. Určite maximálny uhol o ktorý možno pohár nakloniť tak aby sa džús nevylial.
- Klesanie cesty
Dopravná značka informuje o klesaní 6,4%. Vypočítajte pod akým uhlom cesta priemerne klesá. - Cesta
Medzi mestami A a B, vzdialených 7 km má cesta priemerné stúpanie 9‰. Vypočítajte výškový rozdiel miest A a B. - Kocka - uhly
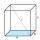Vypočítajte uhol alfa (α) medzi stenovou uhlopriečkou a podstavou kocky. Vypočítajte uhol beta (β) medzi telesovou uhlopriečkou a podstavou kocky. - Sklon trate
Vypočítajte priemerný sklon trate (v promile a aj v stupňoch) z Prievidze (309 m. N. M) do stanice Nitra (167 m. N. M), ak trať je dlhá 77 km. - Uhol sklonu
Nájdite uhol sklonu rampy, ktorá stúpa o 80 cm a je dlhá 200 cm.
- Veža + stožiar
Na vodorovnej rovine je zvislá veža s vlajkovou tyčou na jej vrchole. V bode vzdialenom 9 m od nohy veže je uhol elevácie hornej a dolnej časti vlajkovej tyče 60° a 30°. Nájdite výšku stožiaru vlajky. - Búrka zlomí
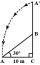Strom sa vplyvom búrky zlomí a zlomená časť sa ohne tak, že sa vrchol stromu dotkne zeme a zviera s ním uhol 30°. Vzdialenosť medzi pätou stromu a bodom, kde sa vrchol dotýka zeme, je 8 m. Nájdite výšku stromu. - Vzdialenosť veže
Pozorovací uhol vrcholu veže od bodu A na zemi je 30°. Pri presune na vzdialenosť 20 m smerom k päte veže do bodu B sa pozorovací uhol zväčší na 60°. Nájdite výšku veže a vzdialenosť veže od miesta A . - Os x a priamka
Nájdite uhol medzi osou x a čiarou spájajúcou body (3, -1) a (4,-2) . - Pozorovací uhol
Z bodu A na zemi je pozorovací uhol vrcholu 20 m vysokej budovy 45°. Na vrchole budovy je vztýčená vlajka a pozorovací uhol vrcholu vlajkovej tyče od A je 60°. Nájdite dĺžku vlajkovej tyče a vzdialenosť budovy od bodu A.
- Pozorovací uhol
Dvaja muži sú na opačných stranách veže. Namerajú uhly elevácie (pozorovací) vrcholu veže ako 30° a druhý ako 45°. Ak je výška veže 50 m, nájdite vzdialenosť medzi týmito dvoma mužmi. - Trojuholník diagram
Podľa nákresu - diagramu - nájdite dĺžky označené h a b. Jeden obdĺžnik a jeden pravouhlý trojuholník zdieľajú jednu stranu. Poznáme dva uhly a dĺžku spoločnej strany, ako je znázornené na obrázku. - Vzdialenosť lode
Muž stojaci na palube lode, ktorá je 10 m nad hladinou vody, pozoruje vrchol kopca pri pozorovacom uhle (elevácie) 60° a pozorovací uhol sklonu päty kopca je 30°. Nájdite vzdialenosť kopca od lode a výšku kopca. - Pilier
Uhol sklonu vrcholu nedokončeného piliera v bode 150 m od jeho základne je 30°. Ak má byť uhol elevácie v tom istom bode 45°, potom sa musí stĺp zdvihnúť do výšky o koľko metrov? - Maják - východ
Maják má výhľad na záliv a je vysoký 77 metrov. Z vrchu môže strážca majáku vidieť jachtu na juh pod hĺbkovým uhlom (uhol depresie) 32 stupňov a ďalšiu loď na východ pod uhlom 25 stupňov. Aká je vzdialenosť medzi člnmi?
Apotém pravidelného šesťuholníka je 5√3 palcov. Nájdite jednu z jeho strán a jeho obsah.Máš úlohu, nad ktorou si lámeš aspoň 10 minút hlavu? Pošli nám úlohu a my Ti ju skúsime vypočítať. Riešenie príkladov z matematiky.
