Kulový vrchlík
Jaký je povrch kulového vrchlíku, základna průměr 21 m, výška 5 m.
Vaše odpověď:
Vaše odpověď:
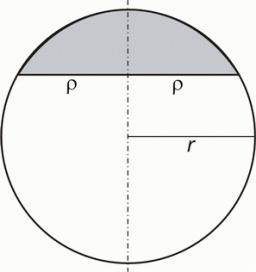
Zobrazuji 1 komentář:
Žák
Jak mám prosím přenést tvar polokoule o průměru koule 8 cm na látku ? děkuji za pomoc Zdeňka Suská
Tipy na související online kalkulačky
Vyzkoušejte také naši kalkulačku pravouhlého trojuholníka.
Chcete zaokrouhlit číslo?
Vyzkoušejte také naši trigonometrickou trojúhelníkovou kalkulačku.
Chcete zaokrouhlit číslo?
Vyzkoušejte také naši trigonometrickou trojúhelníkovou kalkulačku.
K vyřešení této úlohy jsou potřebné tyto znalosti z matematiky:
aritmetikastereometrieplanimetrie
Doporučujeme k tomuto príkladu si prohlédnout toto výukové video: video1
Související a podobné příklady:
- Vrchlík
Jaký je povrch kulového vrchlíku pokud průměr základny je 20 m a výška 2,5 m? - Zahrada - plot
Zahrada tvaru čtverce má ze tří stran živý plot. Jeho délka je 36 metrů. Jaký je obsah zahrady v m²? - Obvod čtvercové krabičky
Obvod krabičky ve tvaru čtverce je 8000 mm. Jaký je rozměr krabičky v m? Zápis, náčrt, výpočet - Nadmořská výška
Určete rozdíl nadmořských výšek vrcholu Sněžky (1 602 m n. M. ) a hladiny Mrtvého moře (-394 m n. M. ). - Konstrukce trojúhelníku
Sestroj trojúhelník KLM pokud strana m=6,5 cm, těžnice tm=4 cm, výška na stranu m: vm=3,2 cm - Vyjádření neznámé n
Z výrazu 2n+m=52 vyjádři neznámou n - Povrch krychle
Vypočítejte povrch krychle v m² když víte, že obsah jejích dvou stěn je 72 dm².
