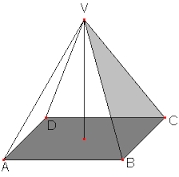
Čtyřboký jehlan 12
Vypočítej objem pravidelného čtyřbokého jehlanu, je-li dáno:
1) a = 3,5 m; vt = 24 dm
Objem vyjádři v m3 a zaokrouhlete na 1 desetinné místo
2) a = 1,6 dm; vt = 295 mm
Objem vypočítej v cm3 a zaokrouhlete na 1 desetinné místo
Zápis řešení:
1) zadání
2) vzoreček
3) dosazení
4) výpočet
Vaše odpověď:
1) a = 3,5 m; vt = 24 dm
Objem vyjádři v m3 a zaokrouhlete na 1 desetinné místo
2) a = 1,6 dm; vt = 295 mm
Objem vypočítej v cm3 a zaokrouhlete na 1 desetinné místo
Zápis řešení:
1) zadání
2) vzoreček
3) dosazení
4) výpočet
Vaše odpověď:
Tipy na související online kalkulačky
Víte objem a jednotku objemu a chcete proměnit jednotku objemu?
K vyřešení této úlohy jsou potřebné tyto znalosti z matematiky:
Související a podobné příklady:
- Obvod čtvercové krabičky
Obvod krabičky ve tvaru čtverce je 8000 mm. Jaký je rozměr krabičky v m? Zápis, náčrt, výpočet - Dosazení do výrazu-vzorce
Dosaď za proměnné a urči hodnotu výrazu: a) x+y+2x-3y. x=1, y = 2 b) a+5b-a+4b. a=8, b=-8 c) mn-5mn+6mn. M=-3, n=-4 d) k+10m+5k-6m+13km. k=1, m=0 - Vyjádření neznámé n
Z výrazu 2n+m=52 vyjádři neznámou n - Ze vzorce 2
Ze vzorce pro výpočet tepelné energie Q=m*c*t vyjádři t a vypočítej, o kolik °C se musí ohřát 2 kg vody, aby se její energie zvýšila o 126 kJ - Voda v bazénu
Kolik litrů vody je v bazénu, jehož šířka je 12 m, délka 25 m a hloubka 280 cm, je-li naplněn 10 cm pod okraj? Jaká je plocha stěn, které smáčí voda (v m2)? - 4b jehlan 4
Vypočítejte povrch pravidelného čtyřbokého jehlanu, je-li dáno: a= 3,2 cm v= 19 cm Postup: 1) výpočet výšky boční stěny 2) obsah podstavy 3) obsah pláště 4) povrch pravidelného čtyřbokého jehlanu - Stěnová výška
Vypočtěte povrch a objem pravidelného čtyřbokého jehlanu, je-li dáno a=6 cm, v=0,8 dm(stěnová výška).
