Geometrie - slovní úlohy a příklady - strana 16 z 37
Počet nalezených příkladů: 735
- Rozděl 6435
Rozděl usecku AB délky 14cm v poměru 5:6 - Lodník
Po palubě lodí kráčí lodník stálou rychlostí 5 km/h ve směru, který svírá se směrem rychlosti lodi úhel 60°. Loď se pohybuje vzhledem ke klidné hladině jezera stálou rychlostí 10 km/h. Určete graficky velikost rychlosti, kterou se lodník pohybuje vzhledem - Směrnice
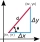Vypočítejte sklon přímky, která prochází body [-35, -65] a [-6, 31]. - Kruhového 7920
Tři bratři byli v chatě na břehu kruhového jezera. Andrej každé ráno oběhl kolem jezera. Současně s ním Braňo skočil před chatou do vody a plaval tak, aby byl vždy ve středu mezi běžícím Andrejem a chatou. Dušan chytal ryby z člunu, který měl ukotven tak, - Úsečku Úsečku dlouhou 4 cm zvětšete v poměru 5/2. Kolik cm bude měřit nová úsečka?
- Vzdálenosti 4529
Chlapec vesluje na loďce rychlostí velikosti 7,2 km/h. Loďku nasměroval kolmo na protilehlý břeh vzdálený 600m. Řeka unáší loďku rychlostí 4,0 km/h. Jaká je výsledná rychlost loďky vzhledem ke břehu? Jak daleko unese řeka loďku od místa, kde by měla loďka - Směrnice
Směrnice (sklon) přímky, jejíž rovnice je 3x +3 = 0, je: - V plánku
Trojúhelníková stavební parcela je na plánu v měřítku 1 : 5 000 zakreslena jako trojúhelník o stranách délek 32,5 mm, 23,5 mm a 36 mm. Určete, kolik m pletiva je potřeba na oplocení celé parcely. - Čtverec
Narýsujte čtverec o hraně a= 4cm. Vyznačte střed souměrnosti S a všechny osy souměrnosti. Kolik os souměrnosti má? Zapište. - Auta
Podle pravidel silničního provozu mohou potkávací světla auta osvětlovat cestu do vzdálenosti maximálně 30 m. Kvůli kontrole dosahu potkávacích světel svého auta zastavil Petr ve vzdálenosti 1,5 m od zdi. Potkávací světla jsou na autě ve výšce 60 cm. V ja - Sestrojte 6770
Je dána kružnice k(S;2,5cm) a bod L pokud |SL|=4cm. Sestrojte tečnu ke kružnici, která prochází bodem L. - Zrychlení ze síl
Na objekt o hmotnosti 10 kg působí síly 60 N - ze severu a 80 N z východu. Jaké je zrychlení objektu? - Úsečka - v poměru
Úsečku dlouhou 8 cm zvětšíme v poměru 7:4. Jak dlouhá v cm bude nová úsečka? - Směrnice RR
Přímka má nárůst o 5 na úseku 4. Jaký je její směrnice (sklon)? - Souřadnicovými 49433
Narysuj graf funkce dané rovnicí y = -2x +3, urč její průsečíky se souřadnicovými osami a doplň chybějící souřadnice A[3;? ], B[? ;8]. - MO - trojúhelníky
Na stranách AB a AC trojúhelníku ABC lěží po řadě body E a F, na úsečce EF leží bod D. Přmky EF a BC jsou rovnoběžné a součastně platí FD : DE = AE : EB = 2:1. Trojúhelník ABC má obsah 27 hektarů a úsečkami EF, AD a DB je rozdělen na čtyři části . Určete - Souřadnice vrcholů
Jsou dány souřadnice vrcholů trojúhelníku: P (-12,6), Q (4,0), R (-8, -6). Načrtněte obrázek trojúhelníku. Najděte obsah trojúhelníku. - Thalet
Jsou dány dva body K a L, KL= 4 cm. Sestroj přímku p, která prochází bodem K a od bodu L má vzdálenost 4 cm. - Tečna
Je dána kružnice k se středem S a poloměrem 3,5cm. Vzdálenost přímky p od středu je 6 cm. Sestrojte tečnu kružnice n, která je kolmá na přímku p - Úhlopříčka deleno tri
V daném obdélníku ABCD je E střed BC a F střed CD. Dokažte, že přímky AE a AF dělí úhlopříčku BD na tři stejné části.
Máš úkol, který jsi tady nenašel vyřešen? Pošli nám úkol a my Ti ji zkusíme vypočítat. Řešení příkladů z matematiky.
