Příklady pro výpočet plošného obsahu tělesa (povrchu tělesa) - strana 16 z 50
Počet nalezených příkladů: 989
- Rotační telesa
 Rotační kužel a rotační válec mají stejný objem 180 cm³ a stejnou výšku v=15cm. Které z těchto dvou těles má větší povrch?
Rotační kužel a rotační válec mají stejný objem 180 cm³ a stejnou výšku v=15cm. Které z těchto dvou těles má větší povrch? - Plechová 2
 Plechová nádrž tvaru kvádru rozměru a=25dm, b=5,6m, c=180cm se bude natírat zvenku. Kolik plechovek barvy musíme koupit a kolik korun zaplatíme, stojí jedna 204,-kč a a stačí na nátření 8,5m2
Plechová nádrž tvaru kvádru rozměru a=25dm, b=5,6m, c=180cm se bude natírat zvenku. Kolik plechovek barvy musíme koupit a kolik korun zaplatíme, stojí jedna 204,-kč a a stačí na nátření 8,5m2 - Čtverečních 22383
 Vodojem má tvar koule o průměru 10m. Kolik hl vody se v něm nachází, když je napuštěn na 90%? Kolik kg barvy je potřebných k natření, pokud se natírá dvakrát a 1kg barvy vystačí na 6 metrů čtverečních?
Vodojem má tvar koule o průměru 10m. Kolik hl vody se v něm nachází, když je napuštěn na 90%? Kolik kg barvy je potřebných k natření, pokud se natírá dvakrát a 1kg barvy vystačí na 6 metrů čtverečních? - Rozhledna 4
 Rozhledna je kryta střechou tvaru pravidelného čtyřbokého jehlanu s podstavnou hranou 8 m a výškou 6 m. 60% krytiny je třeba vyměnit. Kolik m² je třeba zakoupit?
Rozhledna je kryta střechou tvaru pravidelného čtyřbokého jehlanu s podstavnou hranou 8 m a výškou 6 m. 60% krytiny je třeba vyměnit. Kolik m² je třeba zakoupit? - Vypočtěte 12
 Vypočtěte povrch a objem pravidelného devítibokého jehlanu, měří-li poloměr kružnice vepsané podstavě ρ= 12 cm a výška jehlanu je 24 cm
Vypočtěte povrch a objem pravidelného devítibokého jehlanu, měří-li poloměr kružnice vepsané podstavě ρ= 12 cm a výška jehlanu je 24 cm - Papír
 Kolik m² papíru je potřeba na polepení krabice tvaru kvádru o rozměrech 50 cm, 40 cm a 30 cm? Na přehyby připočítej jednu desetinu plochy.
Kolik m² papíru je potřeba na polepení krabice tvaru kvádru o rozměrech 50 cm, 40 cm a 30 cm? Na přehyby připočítej jednu desetinu plochy. - Čtverečních! 32441
 Uzavřenou nádrž na olej tvaru kostky o délce hrany 1,5 metru jsme dvakrát natřeli ochranným nátěrem. Kolik kilogramů barvy jsme spotřebovali, když 1kg barvy vystačí na 10 metrů čtverečních? Kolik litrů oleje je v nádrži, je-li naplněna po okraj?
Uzavřenou nádrž na olej tvaru kostky o délce hrany 1,5 metru jsme dvakrát natřeli ochranným nátěrem. Kolik kilogramů barvy jsme spotřebovali, když 1kg barvy vystačí na 10 metrů čtverečních? Kolik litrů oleje je v nádrži, je-li naplněna po okraj? - Rovnoramenného 6596
 Šperkovnice je tvaru čtyřbokého hranolu s podstavou rovnoramenného lichoběžníku se stranami a se rovná 15 centimetrů b se rovná 9 centimetrů c se rovná 10 centimetrů v se rovná 7 celá 4 centimetru. Kolik látky je potřeba na obtažení šperkovnice pokud její
Šperkovnice je tvaru čtyřbokého hranolu s podstavou rovnoramenného lichoběžníku se stranami a se rovná 15 centimetrů b se rovná 9 centimetrů c se rovná 10 centimetrů v se rovná 7 celá 4 centimetru. Kolik látky je potřeba na obtažení šperkovnice pokud její - Vypočítejte 4842
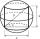 Obsah pláště rotačního válce je polovina obsahu jeho povrchu. Vypočítejte povrch válce, když víte, že úhlopříčka osového řezu je 5cm.
Obsah pláště rotačního válce je polovina obsahu jeho povrchu. Vypočítejte povrch válce, když víte, že úhlopříčka osového řezu je 5cm. - Střecha
 Střecha domu má tvar pravidelného čtyřbokého jehlanu o výšce 5 m a hraně podstavy 7 m. Kolik je třeba tašek o obsahu 540 cm²?
Střecha domu má tvar pravidelného čtyřbokého jehlanu o výšce 5 m a hraně podstavy 7 m. Kolik je třeba tašek o obsahu 540 cm²? - Krabice na mléko
 Monika si změřila rozměry dvou různých krabic na mléko. Jedna měla rozměry 9*5,8*19,6 cm, druhá 9,4*6,3*17,3 cm. Zaujalo ji, zda se na výrobu některé krabice spotřebuje méně materiálu. Ověř to a zjisti, kolik procent materiálu se ušetří. (Materiál na zalo
Monika si změřila rozměry dvou různých krabic na mléko. Jedna měla rozměry 9*5,8*19,6 cm, druhá 9,4*6,3*17,3 cm. Zaujalo ji, zda se na výrobu některé krabice spotřebuje méně materiálu. Ověř to a zjisti, kolik procent materiálu se ušetří. (Materiál na zalo - Vypočítej 39
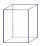 Vypočítej objem (V) a povrch (S) pravidelného čtyřbokého hranolu, jehož výška je 28,6 cm a odchylka tělesové úhlopříčky od roviny podlahy je 50°.
Vypočítej objem (V) a povrch (S) pravidelného čtyřbokého hranolu, jehož výška je 28,6 cm a odchylka tělesové úhlopříčky od roviny podlahy je 50°. - 3B hranol - stan
 Kolik m² látky je třeba na zhotovení stanu pravidelného 3-bokého hranolu pokud je třeba počítat s 2% rezervou látky? Rozměry - 2m 1,6m a výška 1,4m
Kolik m² látky je třeba na zhotovení stanu pravidelného 3-bokého hranolu pokud je třeba počítat s 2% rezervou látky? Rozměry - 2m 1,6m a výška 1,4m - Truhlář
 Kvádr s podstavou a rozměry 12 cm a 5 cm a výšce 4 cm. Truhlář tento kvádr rozřezal na dva shodné trojboké hranoly s podstavami ve tvaru pravoúhlého trojúhelníku. Truhlář vytvořeny hranoly natřel barvou. Vypočítejte povrch jednoho z těchto dvou trojbokých
Kvádr s podstavou a rozměry 12 cm a 5 cm a výšce 4 cm. Truhlář tento kvádr rozřezal na dva shodné trojboké hranoly s podstavami ve tvaru pravoúhlého trojúhelníku. Truhlář vytvořeny hranoly natřel barvou. Vypočítejte povrch jednoho z těchto dvou trojbokých - Administrativní budova
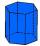 Administrativní budova byla postavena ve tvaru pravidelného šestiúhelníku vepsaného do kružnice s poloměrem 12 m. Výška stěn je 7 m. Kolik Kč stálo omítnutí stěn budovy, jestliže za 1 m čtvereční zaplatíte zedníkům 400 Kč?
Administrativní budova byla postavena ve tvaru pravidelného šestiúhelníku vepsaného do kružnice s poloměrem 12 m. Výška stěn je 7 m. Kolik Kč stálo omítnutí stěn budovy, jestliže za 1 m čtvereční zaplatíte zedníkům 400 Kč? - Věž
 Vypočtěte povrch pravidelného čtyřbokého jehlanu, jehož podstavná hrana měří 6 cm, je-li odchylka roviny boční stěny od roviny podstavy 50 stupňů.
Vypočtěte povrch pravidelného čtyřbokého jehlanu, jehož podstavná hrana měří 6 cm, je-li odchylka roviny boční stěny od roviny podstavy 50 stupňů. - Hranol
 Kolmý hranol, jehož podstavou je pravoúhlý trojúhelník s odvěsnou délky a = 8 cm a přeponou c = 15 cm, má stejný objem jako krychle o hraně délky 1 dm. a) Určete výšku hranolu b) Vypočtěte povrch hranolu c) Kolik procent povrchu krychle je povrch hranolu
Kolmý hranol, jehož podstavou je pravoúhlý trojúhelník s odvěsnou délky a = 8 cm a přeponou c = 15 cm, má stejný objem jako krychle o hraně délky 1 dm. a) Určete výšku hranolu b) Vypočtěte povrch hranolu c) Kolik procent povrchu krychle je povrch hranolu - Osový řez
 Osovým řezem kužele, jehož povrch je 208 m², je rovnostranný trojúhelník. Vypočítejte objem kužele.
Osovým řezem kužele, jehož povrch je 208 m², je rovnostranný trojúhelník. Vypočítejte objem kužele. - Vypočtěte 6
 Vypočtěte povrch a objem pravidelného čtyřbokého jehlanu, je-li hrana dolní podstavy 18 cm a hrana horní podstavy 15 cm. Stěnová výška je 9 cm.
Vypočtěte povrch a objem pravidelného čtyřbokého jehlanu, je-li hrana dolní podstavy 18 cm a hrana horní podstavy 15 cm. Stěnová výška je 9 cm. - Potřebujeme 6021
 Kolik barvy potřebujeme na vymalování bazénu tvaru 6 bokého hranolu, pokud podstavná hrana měří 21 dm, příslušná výška je 1,8 m, výška bazénu je 150 cm. Na 1m² potřebujeme 0,21 kg barvy.
Kolik barvy potřebujeme na vymalování bazénu tvaru 6 bokého hranolu, pokud podstavná hrana měří 21 dm, příslušná výška je 1,8 m, výška bazénu je 150 cm. Na 1m² potřebujeme 0,21 kg barvy.
Máš úkol, který jsi tady nenašel vyřešen? Pošli nám úkol a my Ti ji zkusíme vypočítat. Řešení příkladů z matematiky.
