Kvádr
Kvádr má objem 40 cm3. Kvádr má celkovou plochu 100 cm čtverečních. Jedna hrana kostky má délku 2 cm. Najděte délku úhlopříčky kvádru. Dejte svou odpověď správně na 3 desetinná místa.
Vaše odpověď:
Vaše odpověď:
Tipy na související online kalkulačky
Hledáte pomoc s výpočtem kořenů kvadratické rovnice?
Máte soustavu rovnic a hledáte kalkulačku soustavy lineárních rovnic?
Tip: Převody jednotky objemu vám pomůže naše kalkulačka pro převody jednotek objemu.
Vyzkoušejte také naši kalkulačku pravouhlého trojuholníka.
Vyzkoušejte také naši trigonometrickou trojúhelníkovou kalkulačku.
Máte soustavu rovnic a hledáte kalkulačku soustavy lineárních rovnic?
Tip: Převody jednotky objemu vám pomůže naše kalkulačka pro převody jednotek objemu.
Vyzkoušejte také naši kalkulačku pravouhlého trojuholníka.
Vyzkoušejte také naši trigonometrickou trojúhelníkovou kalkulačku.
K vyřešení této úlohy jsou potřebné tyto znalosti z matematiky:
algebrastereometrieplanimetrieJednotky fyzikálních veličinÚroveň náročnosti úkolu
Doporučujeme k tomuto príkladu si prohlédnout toto výukové video: video1
Související a podobné příklady:
- Zaokrouhlete hřiště
Fotbalové hřiště má délku 101,8 m a šířku 69,8 m. Najděte celkovou plochu pole ve čtverečních metrech (m2) a převeďte tuto míru na čtvereční yardy (yd2). Využijte faktu, že 1 yard = 0,9144 m. Svou odpověď zaokrouhlete na nejbližší celé číslo - Tělesová úhlopříčka
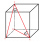Vypočítejte délku tělesové úhlopříčky kvádru o rozměrech 6 cm, 7 cm, 10 cm. Výsledek zaokrouhlete na dvě desetinná místa. - Kvádr/hranol
Urči objem betonovém kvádru jehož jedna hrana podstavy má délku 3 m, tělesová úhlopříčka 13 m a výška 12 m. - Výška = hrana
Kvádr má délku 12 cm, šířku 0,6 dm. Výška má stejnou velikost jako hrana kostky, jejíž objem je 64 cm³. Vypoctej objem kvádru v cm³. - Tělesová úhlopříčka
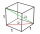Najděte délku tělesové úhlopříčky kvádru s délkou = 20 m šířka = 25 m výška = 150 m - Chyba měření
Student změřil svou třídu a udal šířku 7 m a délku 9 m. Pokud je chyba měření 2 procenta, určete největší hodnotu [X+Y]/X, pokud X a Y jsou šířka a délka třídy. Svou odpověď uveďte na 4 desetinná místa. - Materiál - textil
Kolik metrů čtverečních materiálu je třeba na zhotovení dvou shodných kvádrů o rozměrech 6 dm, 8 dm a 12 dm, pokud počítáme 8% materiálu na záhyby? (Zaokrouhlete na dvě desetinná místa. )
