Příklady pro výpočet plošného obsahu tělesa (povrchu tělesa) - strana 8 z 50
Počet nalezených příkladů: 989
- Dřevěne misky
 20 dřevěných misek tvaru komolého kužele máme natřít zvenku i zevnitř lakem na dřevo. Na natření 200 cm² potřebujeme 0,1 l laku. Kolik litrů laku musíme koupit, pokud jsou misky 25 cm vysoké, dno misky má průměr 20 cm a horní podstava má průměr 30 cm?
20 dřevěných misek tvaru komolého kužele máme natřít zvenku i zevnitř lakem na dřevo. Na natření 200 cm² potřebujeme 0,1 l laku. Kolik litrů laku musíme koupit, pokud jsou misky 25 cm vysoké, dno misky má průměr 20 cm a horní podstava má průměr 30 cm? - Model 3
 Model hradu má střechu ve tvaru kužele. Strana kužele je 45 cm dlouhá a poloměr podstavy je 27 cm. a) Jaký je objem střechy? b) Kolik dm² tapety se spotřebuje na polepení střechy, tedy pláště kužele? c) Jaká je hmotnost střechy, jestliže je vyrobena ze dř
Model hradu má střechu ve tvaru kužele. Strana kužele je 45 cm dlouhá a poloměr podstavy je 27 cm. a) Jaký je objem střechy? b) Kolik dm² tapety se spotřebuje na polepení střechy, tedy pláště kužele? c) Jaká je hmotnost střechy, jestliže je vyrobena ze dř - V rotačním válci
 V rotačním válci je dáno: povrch S = 96 cm² a objem V = 192 cm krychlových. Vypočtěte jeho poloměr a výšku.
V rotačním válci je dáno: povrch S = 96 cm² a objem V = 192 cm krychlových. Vypočtěte jeho poloměr a výšku. - Přesýpací hodiny
 Přesýpací hodiny sestávají ze dvou shodných nádobek ve tvaru rotačních kuželů. Pro jednoduchost předpokládáme, že koužely se dotýkají pouze svými vrcholy. Písek sahá do poloviny výšky spodního kužele. Po překlopení hodí trvá přesně 21 minut, než se písek
Přesýpací hodiny sestávají ze dvou shodných nádobek ve tvaru rotačních kuželů. Pro jednoduchost předpokládáme, že koužely se dotýkají pouze svými vrcholy. Písek sahá do poloviny výšky spodního kužele. Po překlopení hodí trvá přesně 21 minut, než se písek - Bazén - optimalizace
 V rekreační oblasti se má postavit bazén ve tvaru kvádru o objemu 200m³. Jeho délka má být 4-násobkem šířky, přičemž cena 1 m² dna bazénu je 2-krát levnější než 1 m² stěny bazénu. Jaké rozměry musí mít bazén, aby stavba byla nejlevnější?
V rekreační oblasti se má postavit bazén ve tvaru kvádru o objemu 200m³. Jeho délka má být 4-násobkem šířky, přičemž cena 1 m² dna bazénu je 2-krát levnější než 1 m² stěny bazénu. Jaké rozměry musí mít bazén, aby stavba byla nejlevnější? - Koule težké
 Kolik kouli s poloměrem 15 cm se vejde do vetší koule s poloměrem 150 cm?
Kolik kouli s poloměrem 15 cm se vejde do vetší koule s poloměrem 150 cm? - Kostky
 Těleso vzniklo slepením tří shodných kostek. Jeho objem je 192 cm³. Jaký je jeho povrch v dm²?
Těleso vzniklo slepením tří shodných kostek. Jeho objem je 192 cm³. Jaký je jeho povrch v dm²? - Valec
 Objem válce jehož výška se rovná poloměru podstavy je 678,5 dm³. Vypočtete jeho povrch.
Objem válce jehož výška se rovná poloměru podstavy je 678,5 dm³. Vypočtete jeho povrch. - Na válec
 Na válec o průměru 4,6 cm nasaďte část koule tak, aby povrch této části byl 20 cm². Určete r koule ze které byl vrchlík seříznut.
Na válec o průměru 4,6 cm nasaďte část koule tak, aby povrch této části byl 20 cm². Určete r koule ze které byl vrchlík seříznut. - Osmistěn
 Na každé stěně pravidelného osmistěnu je napsáno jedno z čísel 1, 2, 3, 4, 5, 6, 7 a 8, přičemž na různých stěnách jsou různá čísla. U každé stěny Jarda určil součet čísla na ní napsaného s čísly tří sousedních stěn. Takto dostal osm součtů, které také se
Na každé stěně pravidelného osmistěnu je napsáno jedno z čísel 1, 2, 3, 4, 5, 6, 7 a 8, přičemž na různých stěnách jsou různá čísla. U každé stěny Jarda určil součet čísla na ní napsaného s čísly tří sousedních stěn. Takto dostal osm součtů, které také se - Terezka
 Krychle má obsah podstavy 289 mm². Vypočítej její délku hrany, objem a povrh plášte.
Krychle má obsah podstavy 289 mm². Vypočítej její délku hrany, objem a povrh plášte. - Krychle
 Jedna krychle je kouli vepsána a druhá opsána. Vypočítejte rozdíl objemů v obou krychlích, pokud rozdíl jejich povrchů je 231 dm².
Jedna krychle je kouli vepsána a druhá opsána. Vypočítejte rozdíl objemů v obou krychlích, pokud rozdíl jejich povrchů je 231 dm². - Trojboký jehlan
 Vypočítejte objem a povrch pravidelného trojbokého jehlanu, jehož výška je stejná jako délka hrany podstavy 10 cm.
Vypočítejte objem a povrch pravidelného trojbokého jehlanu, jehož výška je stejná jako délka hrany podstavy 10 cm. - Malovka
 Kolik Kč zaplatíte za výmalbu pokoje tvaru kvádru s rozměry podlahy 5 a 4m, když výška pokoje je 3 m. Nebudete malovat podlahu, prostor dveří (210 x 90 cm) a prostor za zrcadlem (rovnostranný trojúhelník se stranou 4 dm). Chcete udělat dvojitý nátěr, vyda
Kolik Kč zaplatíte za výmalbu pokoje tvaru kvádru s rozměry podlahy 5 a 4m, když výška pokoje je 3 m. Nebudete malovat podlahu, prostor dveří (210 x 90 cm) a prostor za zrcadlem (rovnostranný trojúhelník se stranou 4 dm). Chcete udělat dvojitý nátěr, vyda - Kornout
 Kolik cm² těsta je třeba na výrobu zmrzlinového kornoutu, má-li se do něj vejít 0,3l zmrzliny a jeho výška má být 15 cm. Připočti 8% na přehyby. 1. Převeď litry na cm³ 2. Rozhodni, jaký údaj můžeš dopočítat jako první a z jakého vzorce. 3. Vypočítej údaj
Kolik cm² těsta je třeba na výrobu zmrzlinového kornoutu, má-li se do něj vejít 0,3l zmrzliny a jeho výška má být 15 cm. Připočti 8% na přehyby. 1. Převeď litry na cm³ 2. Rozhodni, jaký údaj můžeš dopočítat jako první a z jakého vzorce. 3. Vypočítej údaj - Vypočítejte 34
 Vypočítejte povrch a objem válce s poloměrem podstavy 5 cm a výškou 8 cm.
Vypočítejte povrch a objem válce s poloměrem podstavy 5 cm a výškou 8 cm. - Koule ve kuželi
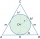 Do kužele je vepsána koule (průnik jejich hranic se skládá z kružnice a jednoho bodu). Poměr povrchu koule a obsahu podstavy je 4:3. Rovina, která prochází osou kužele, řeže kužel v rovnoramenném trojúhelníku. Určete velikost úhlu oproti základně tohoto t
Do kužele je vepsána koule (průnik jejich hranic se skládá z kružnice a jednoho bodu). Poměr povrchu koule a obsahu podstavy je 4:3. Rovina, která prochází osou kužele, řeže kužel v rovnoramenném trojúhelníku. Určete velikost úhlu oproti základně tohoto t - Tapeta
 Vypočítej, kolik m² tapety je třeba k vytapetování místnosti o rozměrech a = 3m, b = 4m, a výškou c = 3,5m
Vypočítej, kolik m² tapety je třeba k vytapetování místnosti o rozměrech a = 3m, b = 4m, a výškou c = 3,5m - 4-boký jehlan v2
 Vypočítejte objem a povrch pravidelného čtyřbokého jehlanu, jeli obsah podstavy 20 cm². Odchylka boční hrany od roviny podstavy je 60 stupňů.
Vypočítejte objem a povrch pravidelného čtyřbokého jehlanu, jeli obsah podstavy 20 cm². Odchylka boční hrany od roviny podstavy je 60 stupňů. - Kvádr težší
 Kvádr má objem 32 cm³. Jeho plášť má dvojnásobný obsah než jedna ze čtvercových podstav. Jakou délku má tělesová úhlopříčka?
Kvádr má objem 32 cm³. Jeho plášť má dvojnásobný obsah než jedna ze čtvercových podstav. Jakou délku má tělesová úhlopříčka?
Máš úkol, který jsi tady nenašel vyřešen? Pošli nám úkol a my Ti ji zkusíme vypočítat. Řešení příkladů z matematiky.
