Příklady pro středoškoláky - strana 36 z 225
Počet nalezených příkladů: 4490
- Je dána 6
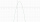Je dána kvadratická funkce: y=-x²+2x+3 a) urči průsečíky s osou x, y a vrchol V b) načrtni graf a popiš c) pro které x platí f(x)=3 - Šest atrakcí - pouti
Kolik máte možností, chcete-li na pouti absolvovat deset jízd, ale je zde pouze šest atrakcí? - Premiéra filmu
Jak můžete rozdělit 40 lístků na premiéru mezi 15 lidí? - Součet a rozdíl
Součet dvou čísel je 18, jejich rozdíl je 10. Která jsou čísla? Vypočítej aritmetický průměr součinu a podílu těchto čísel. - Aleš vs Blanka
Aleš a Blanka si koupili stejnou knihu která měla 240 stran. Blanka četla 4 strany víc denně než Aleš . Blanka ji dočetla dříve než Aleš . Aleš četl knihu oba vykendovy dny déle. Užitím rovnice nebo soustavy rovnic vypočtěte, kolik stran knihy četl denně - Železné trubky
Železné trubky jsou uloženy v 10 řadách nad sebou tak, že v nejvyšší horní řadě je 15 trubek a v každé další je o 1 trubku více. Kolik je všech trubek? - Nákup domu
Konečně jste našli svůj vysněný domov. Prodává se za 120 000 dolarů a lze jej koupit zaplacením 10 % a financováním zůstatku s roční sazbou 9,6 % složeným měsíčně. a) Kolik jsou vaše platby, pokud platíte měsíčně po dobu 30 let? b) Určete, kolik byste zap - Palivo - účinnost
Gravimetrická analýza antracitového paliva je 90 % uhlíku, 3 % vodíku, 2 % kyslíku, 1 % dusíku. Vzhledem k tomu, že objemová analýza produktů suchého spalování je 16,2 % CO2, 3,5 % O2, 80,3 % N2, během spalovacího procesu antracitu, který je považován za - Francescin plat
Francesca vydělává každý rok plat, který je o 2 procenta vyšší než její předchozí rok. Za prvních 5 let v této práci vydělala celkem 187 345 dolarů. Jaký byl Francescin plat v prvním roce v této práci? - Vklad
Za jakou dobu vzroste vklad 2000 € při úrokové míře 4,6% p.. a. na 2500 €? (Ideálně vypočítejte bez logaritmů) - Naspořená částka
Osoba si vkládá 5000 eur na bankovní účet na začátku každého roku po dobu 10 let. Žádné jiné vklady ani výběry z účtu nedělá. Určete celkovou naspořenou částku při složeném ročním 8 % úročení, když se úroky připisují ročně. - Geometrická posloupnost
Součet 2. a 3. člena geometrické posloupnosti je šestinásobek 4. člena. Najděte dvě možné hodnoty společného poměru B, je-li druhý člen 8 a společný poměr je kladný. Najděte prvních 6 výrazů. - Součet Součet prvních 6 členů aritmetické posloupnosti je 552 a součet prvních 2 členů téže posloupnosti je 200. Určete součet prvních 15 členů.
- Odhadněte odmocninu
Odhadněte √38 s přesností na setiny pomocí kterékoli ze dvou metod (metoda dělení a průměru nebo vzorec pro odhad druhé odmocniny). - Zvedání kamene
Člověk zvedá kámen o hmotnosti 285kg s pomocí páky, která je podepřena ve vzdálenosti 30cm od kamene. Člověk působí na páku ve vzdálenosti 90cm od podpěry. Jak velkou sílu musí člověk vynaložit na zvednutí kamene? - 1.soucastka
1.soucastka je polovina. 2 součástka je 2/3 z 1/2. 3 součástka váží 3 kg. Kolik váží jednotlivé součástky a kolik je to dohromady? - Jakosti
V horním sadu bylo sebráno 60% jablek první jakosti, v dolním sadu 90% jablek první jakosti. Kolika % první jakosti bylo dosaženo celkem, jestliže celková úroda činila 240 tun jablek a v dolním sadu byla úroda o 40% bohatší? - Velikost síly
Na kouli o hmotnosti 100 g která leží na vodorovné desce, působí ve vodorovném směru síla, která jí uděluje zrychlení 20 cm. s^ -2 Určete velikost síly. - Newtonův zákon
S jak velkým zrychlením se rozjíždí vlak o hmotnosti 800 t, je-li tažná síla lokomotivy 2*105 N? - Určete 23
Určete odhad intervalu směrodatné odchylky průměrné doby hledání místa na parkování. Jestliže jsme z průzkumu u 200 obyvatel zjistili, že průměrná doba je hodina a 25 minut a směrodatná odchylka 15 minut. Použijte 1% hladinu významnosti.
Máš úkol, který jsi tady nenašel vyřešen? Pošli nám úkol a my Ti ji zkusíme vypočítat. Řešení příkladů z matematiky.
