Tangens - příklady - strana 5 z 15
Počet nalezených příkladů: 293
- Úhel úhlopříčky
V pravidelném 4-bokem jehlanu zvíře boční hrana s úhlopříčkou podstavy úhel 55°. Délka boční hrany je 8 m. Vypočtěte povrch a objem jehlanu. - Jehlan
Pravidelný 4-boky jehlan má tělesových výšku 2 dm a protilehlé boční hrany svírají úhel 70°. Vypočtěte povrch a objem jehlanu. - Podstavou
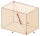Podstavou čtyřbokého hranolu je obdélník o rozměrech 3 dm a 4 dm. Výška hranolu je 1 m. Zjistěte jaký úhel svíra tělesová úhlopříčka s úhlopříčkou podstavy. - Těleso
Těleso se klouže dolů po nakloněné rovině svírající s vodorovnou rovinou úhel α = π / 4 = 45° za účinku sil tření se zrychlením a = 2,4 m/s². Pod jakým úhlem β musí být nakloněná rovina, aby se těleso po ní klouzaly po malém postrčení konstantní rychlostí - Tangens úhlu rovnoběžníku
Je-li ∠BAD mezi stranami AB a AD rovnoběžníku θ, co je pak tan θ? Viz diagram: A=(7,1) B=(5,-2) C=(12,1) D=(14,4) - Rozhledna a turista
Jak daleko od rozhledny vysoké 48 m stal turista, pokud její vrchol viděl pod úhlem o velikosti 40°? - Komolý jehlan
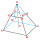Vypočítejte objem pravidelného 4-bokeho komolého jehlanu, jestliže a1 = 14 cm, a2 = 8 cm a úhel, který svírá boční stěna s podstavou je 42 stupňů. - Výška
Výška v a základny a, c v lichoběžníku ABCD jsou v poměru 1:6:3, jeho obsah S = 324 cm čtverečních. Úhel u vrcholu B = 35 stupňů. Určete obvod lichoběžníku - Boční stěna - jehlan
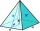Vypočítejte objem jehlanu, jehož hrana podstavy a = 8cm a boční stěna svírá se čtvercovou podstavou úhel α = 60°. - Vypočtěte 12
Vypočtěte povrch a objem pravidelného devítibokého jehlanu, měří-li poloměr kružnice vepsané podstavě ρ= 12 cm a výška jehlanu je 24 cm - Schodiště 4
Schodiště má celkovou výšku 3,6 m a svírá s vodorovnou rovinou úhel o velikosti 26°. Vypočítej délku celého schodiště. - Vypočtěte 10
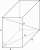Vypočtěte velikost odchylky tělesové úhlopřičky a boční hrany c kvádru o rozměrech: a=28cm, b=45cm a c=73cm. Dále vypočtěte velikost odchylky tělesové úhlopřičky od roviny podstavy. - Pravidelný 8 Pravidelný čtyřboký jehlan má podstavnou hranu a=1,56 dm a výšku v= 2,05dm. Vypočtěte : a) odchylku roviny boční stěny od roviny podstavy b) odchylku boční hrany od roviny podstavy
- Rotační 15
Rotační kužel má poloměr podstavy r=226mm, odchylka strany od roviny podstavy je 56°. Vypočtěte výšku kuželu. - Dotyčnice
Najděte velikost úhlu, pod kterým je elipsa x² + 5 y² = 5 viditelná z bodu P [5, 1]. - Čtyřboký hranol
Výška pravidelného čtyřbokého hranolu je v = 10 cm, odchylka tělesových úhlopříčky od podstavy je 60°. Určete délku podstavových hran, povrch a objem kvádru. - Úhel stoupání cesty
Rovná cesta má stoupání 19%. Jak velký je úhel stoupání? - 12 úhelník
Vypočtěte obsah pravidelného 12 úhelníka, je-li jeho strana a=12 cm. - Vepsaná a opsaná
Vypočítejte poloměry kružnice vepsané a opsané pravidelnému pětiúhelníku, jehož strana měří 3 cm. - Koule ve kuželi
Do kužele je vepsána koule (průnik jejich hranic se skládá z kružnice a jednoho bodu). Poměr povrchu koule a obsahu podstavy je 4:3. Rovina, která prochází osou kužele, řeže kužel v rovnoramenném trojúhelníku. Určete velikost úhlu oproti základně tohoto t
Máš příklad z matematiky, který jsi tady nenašel vyřešený? Pošli nám příklad a my Ti ho zkusíme vypočítat.
