Těleso

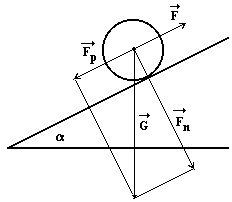
Těleso se klouže dolů po nakloněné rovině svírající s vodorovnou rovinou úhel α = π / 4 = 45° za účinku sil tření se zrychlením a = 2,4 m/s2. Pod jakým úhlem β musí být nakloněná rovina, aby se těleso po ní klouzaly po malém postrčení konstantní rychlostí?

Správná odpověď:

B =  33,1853 °

Postup správného řešení:

α=4π​=43,1416​≐0,7854 rad a=2,4 m/s2 g=9,81 m/s2   G = m g F1​ = m a = m⋅ g ⋅  sin α − m⋅ g⋅ k⋅ cos α m a = m⋅ g ⋅  sin α − m⋅ g⋅ k⋅ cos α a = g ⋅  sin α − g⋅ k⋅ cos α  k=(g⋅ sinα−a)/(g⋅ cosα)=(9,81⋅ sin0,7854−2,4)/(9,81⋅ cos0,7854)≐0,654  a2​=0 m/s2  g ⋅  sin β − g⋅ k⋅ cos β = 0 sin β − k⋅ cos β = 0 sin β/cos β − k= 0 tg β − k= 0  β=arctgk=arctg0,654≐0,5792 rad  B=β→  °=β⋅ π180​   °=0,5792⋅ π180​   °=33,185  °=33,1853∘=33°11′7"

Zkusit jiný příklad


Našel jsi chybu či nepřesnost? Klidně nám ji napiš.







Tipy na související online kalkulačky
Vyzkoušejte také naši kalkulačku pravouhlého trojuholníka.
Vyzkoušejte také naši trigonometrickou trojúhelníkovou kalkulačku.
Vyzkoušejte si převody jednotek úhlů úhlové stupně, minuty, sekundy, radiány.

K vyřešení této úlohy jsou potřebné tyto znalosti z matematiky:

Jednotky fyzikálních veličin:

Téma:

Úroveň náročnosti úkolu:


 
Doporučujeme k tomuto príkladu si prohlédnout toto výukové video: video1

Související a podobné příklady: