Úhel - slovní úlohy a příklady - strana 14 z 60
Počet nalezených příkladů: 1195
- Vepsány čtyřúhelník
Do kružnice je vepsán čtyřúhelník tak, že jeho vrcholy dělí kružnici 1:2:3:4. Vypočítejte velikosti jeho vnitřních úhlů. - Úhel BSA
Je dána kružnice k (S; r) a bod A, který leží na této kružnici. Na obvodu leží také bod B, pro který platí, že je v jednom směru pětkrát dál od bodu A, než v opačném směru (po obvodu kružnice). Určete velikost konvexního úhlu BSA. - Jak velký 2
Jak velký je poloměr kruhové výseče, jejíž středový úhel má velikost 36° a obsah S = 53,095 cm2 - Čtvrtkruh 5 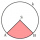Čtvrtkruh s poloměrem 4 má stejný obsah jako kruhová výseč o poloměru 3. Jaká je velikost středového úhlu výseče?
- Vypočtěte úseč
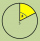Vypočtěte obsah kruhové úseče, je-li poloměr r = 80 cm a středový úhel má velikost α = 110°? - Úhel mezi silami
V jednom bodě působí dvě síly o velikosti 8 Newtonů a 15 Newtonů. Pokud je výsledná síla 17 Newtonů, najděte úhel mezi silami. - Ochlazení vodiče
Měděný vodič má při teplotě 36°C odpor 2,8Ω. Jakou hodnotu odporu bude mít po ochlazení na -22°C? - Úhly v trojúhelníku
Dva úhly trojúhelníku mají stejnou velikost a třetí je o 45 stupňů větší než velikost každého z ostatních dvou. Najděte velikost největšího úhlu v trojúhelníku. - Změna teploty v čase
V 6:00 byla teplota -5 stupňů Celsia. Každou hodinu během šesti hodin se zvyšoval rychlostí o tři stupně. Teplota se pak zvyšovala o 1 1/2° každou hodinu po dobu pěti hodin. Jaká byla teplota v 17:00? - Na kružnici
Na kružnici o poloměru 10 cm a se středem S jsou dány body A, B, C tak, že středový úhel ASB má 60 stupňů a středový úhel ASC má 90 stupňů. Určete délku oblouku kružnice a velikost posunutí AB a AC. - Konstrukce trojúhelníku KLM
Sestrojte trojúhelník KLM kde strana k má 6,7cm; těžnice na stranu k je 4,1cm a úhel LKM má 63 stupňů. Napište postup konstrukce. - Most šikmo přes řeku
Šířka řeky je 89 m. Z terénních důvodů se most odklání od společné kolmice k oběma břehům o úhel 12°30'. Vypočtěte, o kolik metrů je most delší než řeka. - Rovnoramenný
Rovnoramenný lichoběžník ABCD má základny 18 cm a 12 cm. Úhel u vrcholu A má velikost 60°. Jaký je obvod a obsah lichoběžníku? - Na turistické
Na turistické mapě s měřítkem 1:50000 je úsek železniční trati mezi Bobrovou Lhotou a Javořištěm nahrazen obloukem kružnice s poloměrem 6 cm. Oblouk je 90°. Určete skutečnou délku trati mezi oběma vesnicemi. - Růstová křivka
Jaký je ne-trigonometrický vzorec (ne polynomní přizpůsobení) pro růstovou křivku, který algebraicky řeší nárůst mezi tan(1 stupeň), tan(2 stupně) pokračující až po tangentu (45 stupňů)? v pořádku je použít pi. Zkontrolujte výpočet pro 32° - Násobení komplexních čísel
Vyhodnoťte násobení dvou komplexních čísel v cis zápisu: (6 cis 120°) (4 cis 30°) Výsledek zapište v cis a Re-Im notaci. - Výpočet 20
Vypočtěte součet 1/5 pravého úhlu, 3/4 pravého úhlu a 3/4 přímého úhlu. - Doplňkové úhly
Úhly (a + 30)° a (2a)° jsou mírou dvou doplňkových úhlů. Najděte hodnotu a. - Obsah rovnoramenného lichoběžníku
V rovnoramenném lichoběžníku ABCD známe: AB||CD, |CD| = c = 8 cm, výška h = 7 cm, | CAB| = 35°. Najděte obsah lichoběžníku. - Obvod kosočtverce
Jeden z vnitřních úhlů kosočtverce je 120° a kratší úhlopříčka je dlouhá 3,4 metru. Najděte obvod kosočtverce.
Máš úkol, který jsi tady nenašel vyřešen? Pošli nám úkol a my Ti ji zkusíme vypočítat. Řešení příkladů z matematiky.
