Úměra, poměr - slovní úlohy a příklady - strana 13 z 69
Počet nalezených příkladů: 1369
- Obvod a obsah
Pokud víte, že poměr obvodu kruhu a obsahu kruhu je 4:9 Potom průměr kruhu je : - Vzdálenosti 69734
Zvuk se šíří rychlostí 1km za 3 vteřiny. pokud hřmění slyšet 12 sekund po blesku, v jaké vzdálenosti je bouře? - Dům má
Dům má dvě podlaží. Na každém podlaží bydlí muži a ženy v takovém počtu, že jejich poměr je na každém podlaží 3:2. Na druhém podlaží bydlí o pět osob více, než na prvním podlaží. Kolik žen bydlí na druhém podlaží? - Michalovci 69494
Kolik různých průběhů mohl mít zápas mezi AC Michalovci a Juventem Turiecem, který skončil 2:1? - Jak rozdělís
Jak rozdělís tyč dlouhou 3m v poměru 1:5? Délku obou dílů uved v cm. - Trojúhelníku 69144
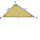Přímka p prochází těžištěm T trojúhelníku a je rovnoběžná s úsečkou BC. Jaký je podíl obsahu rozdělené menší části trojúhelníku přímkou p a obsahu trojúhelníku? - Tříciferných 69114
Kolik je tříciferných čísel, která mají ciferný součet 6? Zapiš poměr počtu vytvořených sudých a lichých čísel a uprav jej na základní tvar.
- Rozdělili 68774
Jana, Martina a Zuzka si rozdělili bonbóny v poměru 3:7:5. Martina dostala o 9 bonbonů méně než měli Jana a Zuzka spolu. Které tvrzení je pravdivé? A. Martina dostala méně bonbonů než Zuzka. B. Všechny spolu dostaly 135 bonbonů. C. Martina dostala o 16 bo - Lichoběžníku 68714
Délka mediánu (střední příčky) lichoběžníku je 10 palců. Medián rozděluje lichoběžník na dvě oblasti, jejichž poměr je 3:5. Délka kratší základny je: - Trojúhelníku 68394
Velikosti vnitřních úhlů trojúhelníku jsou v poměru 3:4:5. Vypočítejte tyto úhly. - Sobotkovi
Sobotkovi při odletu na dovolenou kontrolovali své kufry k odbavení. Čtyři jejich kufry měly hmotnost 3 : 4 : 5 : 8. Celková hmotnost všech čtyř kufrů byla 60 kg. Maximální povolená hmotnost jednoho zavazadla je 25 kg. a) Vypočtěte v kg hmotnost nejlehčíh - Trojčata
Trojčata Jana, Jan a Jitka si naspořila dohromady 180 Kč. Jana má naspořen trojnásobek oproti každému ze svých dvou sourozenců. Jitka a Jan mají naspořenou stejnou částku. a) Určete, v jakém poměru jsou naspořené částky všech tří sourozenců v pořadí Jan, - Ve čtvrtek
Ve čtvrtek bylo třeba přepravit 240 lyžařů, dvěma autobusy trvala přeprava 30 minut. Jak dlouho trvala přeprava v sobotu, jestliže na sjezdovce bylo 660 lyžařů a byly nasazeny 3 autobusy? - Pan Filip
Pan Filip připravuje rekonstrukci zahrady. Rozdělí její plochu na bylinkovou, zeleninovou a okrasnou část v poměru 2 : 3 : 5 (v tomto pořadí). Výměra bylinkové části bude 4m x 2,5 m. a) Vypočtěte v m2, jaká bude celková rozloha zrekonstruované - Slitina Cu+Pb
Slitina mědi a olova je směsí těchto kovů v poměru 5 : 2 (v daném pořadí). Vypočtěte v kg, jakou hmotnost má kus této slitiny, je-li v něm právě o 150 kg méně olova než mědi.
- Bakterie 67644
Bakterie ve zkumavce se dělí každou sekundu na dvě, přičemž každá nová má stejný objem jako původní. Přesně o půlnoci byla zkumavka plná. V kolik hodin byla zkumavka zaplněna do poloviny? - Výrobce 4
Výrobce auta uvádí, že auto spotřebuje průměrně 6,8l benzinu na 100km. Kolik litrů benzinu spotřebuje na cestu dlouhou 348 km? - Paní prodává
Paní prodává oříšky. Má dvě směsi oříšků (kešu/buraky) v poměru 2 : 1 a 1 : 3 (kešu a buráky). Určete v jakém poměru smíchat obě směsi, aby ve výsledné směsi byl poměr kešu/buraky 1 : 2? (Prosím o vysvědčení na jakém principu se toto počítá) - V obci
V obci se pořádá karneval. Poměr ceny jedné dětské vstupenky a ceny jedné vstupenky pro dospělého je 3:4 (v tomto pořadí). Dvě dětské vstupenky a tři vstupenky pro dospělého stojí dohromady 270,- Kč. Kolik celkem zaplatí za vstupenky na karneval 2 dospělí - Podmínky 66544
Mám krabici, ve které jsou bonbony z bílé, mléčné a hořké čokolády, Poměr bonbonů bílých k mléčnými je 3:4. Poměr bonbónů bílých k tmavým je 4:3. Nejméně kolik bonbonů je v krabici, jsou-li splněny podmínky poměrů bonbonů.
Máš příklad, nad kterým si přemýšlíš alespoň 10 minut? Pošli nám příklad a my Ti ho zkusíme vypočítat.
Vyzkoušejte naši kalkulačka na přepočet poměru.
