Cross-sections of a cone
Cone with base radius 16 cm and height 11 cm divided by parallel planes to base into three bodies. The planes divide the height of the cone into three equal parts.
Determine the volume ratio of the maximum and minimum of the resulting body.
Determine the volume ratio of the maximum and minimum of the resulting body.
Correct answer:
Tips for related online calculators
You need to know the following knowledge to solve this word math problem:
Units of physical quantities:
Grade of the word problem:
Related math problems and questions:
- Quadrilateral 81385
 A regular quadrilateral pyramid with base edge length a = 15cm and height v = 21cm is given. We draw two planes parallel to the base, dividing the height of the pyramid into three equal parts. Calculate the ratio of the volumes of the 3 bodies created.
A regular quadrilateral pyramid with base edge length a = 15cm and height v = 21cm is given. We draw two planes parallel to the base, dividing the height of the pyramid into three equal parts. Calculate the ratio of the volumes of the 3 bodies created. - Cutting cone
 A cone with a base radius of 10 cm and a height of 12 cm is given. At what height above the base should we divide it by a section parallel to the base so that the volumes of the two resulting bodies are the same? Express the result in cm.
A cone with a base radius of 10 cm and a height of 12 cm is given. At what height above the base should we divide it by a section parallel to the base so that the volumes of the two resulting bodies are the same? Express the result in cm. - A cone 4
 A cone with a radius of 10 cm is divided into two parts by drawing a plane through the midpoint of its axis parallel to its base. Compare the volumes of the two parts.
A cone with a radius of 10 cm is divided into two parts by drawing a plane through the midpoint of its axis parallel to its base. Compare the volumes of the two parts. - Right circular cone
 The volume of a right circular cone is 5 liters. The cone is divided by a plane parallel to the base, one-third down from the vertex to the base. Calculate the volume of these two parts of the cone.
The volume of a right circular cone is 5 liters. The cone is divided by a plane parallel to the base, one-third down from the vertex to the base. Calculate the volume of these two parts of the cone.
- Cone
 Into rotating cone with dimensions r = 8 cm and h = 8 cm is an inscribed cylinder with maximum volume so that the cylinder axis is perpendicular to the cone's axis. Determine the dimensions of the cylinder.
Into rotating cone with dimensions r = 8 cm and h = 8 cm is an inscribed cylinder with maximum volume so that the cylinder axis is perpendicular to the cone's axis. Determine the dimensions of the cylinder. - A sphere
 A sphere has a radius of 5.5 cm. Determine its volume and surface area. A frustum of the sphere is formed by two parallel planes. One through the diameter of the curved surface of the frustum is to be of the surface area of the sphere. Find the height and
A sphere has a radius of 5.5 cm. Determine its volume and surface area. A frustum of the sphere is formed by two parallel planes. One through the diameter of the curved surface of the frustum is to be of the surface area of the sphere. Find the height and - Cylindrical container
 An open-topped cylindrical container has a volume of V = 3140 cm³. Find the cylinder dimensions (radius of base r, height v) so that the least material is needed to form the container.
An open-topped cylindrical container has a volume of V = 3140 cm³. Find the cylinder dimensions (radius of base r, height v) so that the least material is needed to form the container. - Cone
 The circular cone of height 15 cm and volume 5699 cm³ is at one-third of the height (measured from the bottom) cut by a plane parallel to the base. Calculate the radius and circumference of the circular cut.
The circular cone of height 15 cm and volume 5699 cm³ is at one-third of the height (measured from the bottom) cut by a plane parallel to the base. Calculate the radius and circumference of the circular cut. - Rotating cone
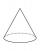 Calculate the volume of a rotating cone with base radius r=$r cm and height h=$v cm.
Calculate the volume of a rotating cone with base radius r=$r cm and height h=$v cm.
- Maximum of volume
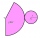 The shell of the cone is formed by winding a circular section with a radius of 1. For what central angle of a given circular section will the volume of the resulting cone be maximum?
The shell of the cone is formed by winding a circular section with a radius of 1. For what central angle of a given circular section will the volume of the resulting cone be maximum? - Sphere in cone
 A sphere of radius 3 cm describes a cone with minimum volume. Determine cone dimensions.
A sphere of radius 3 cm describes a cone with minimum volume. Determine cone dimensions. - Inscribed 6155
 A cylinder with a height equal to half the height of the cone is inscribed in the rotating cone. Find the volume ratio of both bodies.
A cylinder with a height equal to half the height of the cone is inscribed in the rotating cone. Find the volume ratio of both bodies. - Volume of the cone
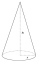 Find the volume of the cone with the base radius r and the height v. a) r = 6 cm, v = 8 cm b) r = 0,9 m, v = 2,3 m c) r = 1,4 dm, v = 30 dm
Find the volume of the cone with the base radius r and the height v. a) r = 6 cm, v = 8 cm b) r = 0,9 m, v = 2,3 m c) r = 1,4 dm, v = 30 dm - Cone
 The circular cone has height h = 29 dm and base radius r = 3 dm slice plane parallel to the base. Calculate the distance of the cone vertex from this plane if solids have the same volume.
The circular cone has height h = 29 dm and base radius r = 3 dm slice plane parallel to the base. Calculate the distance of the cone vertex from this plane if solids have the same volume.
- Cylinder-shaped 81512
 A truncated cone-shaped part with base radii of 4 cm and 22 cm is to be recast into a cylinder-shaped part of the same height as the original part. What base radius will the new part have?
A truncated cone-shaped part with base radii of 4 cm and 22 cm is to be recast into a cylinder-shaped part of the same height as the original part. What base radius will the new part have? - 2x cone
 Circular cone height 84 cm was cut plane parallel with the base. The volume of these two small cones is the same. Calculate the height of the smaller cone.
Circular cone height 84 cm was cut plane parallel with the base. The volume of these two small cones is the same. Calculate the height of the smaller cone. - Cylinder-shaped 4411
 A cylinder-shaped hole with a diameter of 12 cm is drilled into a block of height 50 cm with a square base with an edge length of 20 cm. The axis of this opening passes through the center of the base of the cuboid. Calculate the volume and surface area of
A cylinder-shaped hole with a diameter of 12 cm is drilled into a block of height 50 cm with a square base with an edge length of 20 cm. The axis of this opening passes through the center of the base of the cuboid. Calculate the volume and surface area of
