Probabilities
If probabilities of A, B, and A ∩ B are P (A) = 0.62, P (B) = 0.78, and P (A ∩ B) = 0.26, calculate the following probability (of the union. intersect and opposite and its combinations):
Correct answer:
Tips for related online calculators
Would you like to compute the count of combinations?
You need to know the following knowledge to solve this word math problem:
Related math problems and questions:
- Two doctors
 Doctor A will determine the correct diagnosis with a probability of 89% and doctor B with a probability of 75%. Calculate the probability of proper diagnosis if both doctors diagnose the patient.
Doctor A will determine the correct diagnosis with a probability of 89% and doctor B with a probability of 75%. Calculate the probability of proper diagnosis if both doctors diagnose the patient. - Shooters
 In the army, regiments are six shooters. The first shooter target hit with a probability of 49%, next with 75%, 41%, 20%, 34%, 63%. Calculate the probability of target hit when shooting all at once.
In the army, regiments are six shooters. The first shooter target hit with a probability of 49%, next with 75%, 41%, 20%, 34%, 63%. Calculate the probability of target hit when shooting all at once. - Salami
 We have six kinds of salami that have ten pieces and one kind of salami that has four pieces. How many ways can we distinctly choose five pieces of salami?
We have six kinds of salami that have ten pieces and one kind of salami that has four pieces. How many ways can we distinctly choose five pieces of salami? - Probabilities 71194
 We have a dummy die where numbers fall with probabilities P (1)=0.1; P (2)=0.2; P (3)=0.22; P (4)=0.16; P (5)=0.24; P (6)=0.08. Determine the probability that the two tosses the same numbers.
We have a dummy die where numbers fall with probabilities P (1)=0.1; P (2)=0.2; P (3)=0.22; P (4)=0.16; P (5)=0.24; P (6)=0.08. Determine the probability that the two tosses the same numbers.
- Median of odd count
 The following are the weights (in kg) of seven people: 70, 62, 62, 75, 60, 65, and 78. Find the median of the weights of people.
The following are the weights (in kg) of seven people: 70, 62, 62, 75, 60, 65, and 78. Find the median of the weights of people. - Nursing school
 The following table shows 1000 nursing school applicants classified according to scores made on a college entrance examination and the quality of the high school from which they graduated, as rated by a group of educators: Quality of High Schools Score;
The following table shows 1000 nursing school applicants classified according to scores made on a college entrance examination and the quality of the high school from which they graduated, as rated by a group of educators: Quality of High Schools Score; - And-or probabilities
 P(A ) = 0.53, P(B) = 0.15, and P(A n B ) = 0.18. Find P(A U B ). Round approximations to two decimal places.
P(A ) = 0.53, P(B) = 0.15, and P(A n B ) = 0.18. Find P(A U B ). Round approximations to two decimal places. - Grade point average
 The average GPA is 2.78, with a standard deviation of 0.45. If GPA is normally distributed, what percentage of the students have the following GPAs? Solve for the z-score and report the appropriate percentage: a. Less than 2.30 b. Less than 2.00 c. More t
The average GPA is 2.78, with a standard deviation of 0.45. If GPA is normally distributed, what percentage of the students have the following GPAs? Solve for the z-score and report the appropriate percentage: a. Less than 2.30 b. Less than 2.00 c. More t - Corresponding 33321
 The following data on the height and the corresponding number of pupils were found in the measurement of 63 pupils: 159cm-1,161cm-1,162cm-2,163cm-1,164cm-2,165cm-2,166cm-3,167cm-2,167cm-3 6,172cm-7,173cm-9,174cm -5,175cm-2,177cm-1,178cm-4,179cm-2,181cm-1,
The following data on the height and the corresponding number of pupils were found in the measurement of 63 pupils: 159cm-1,161cm-1,162cm-2,163cm-1,164cm-2,165cm-2,166cm-3,167cm-2,167cm-3 6,172cm-7,173cm-9,174cm -5,175cm-2,177cm-1,178cm-4,179cm-2,181cm-1,
- Sum on dice
 We have two dice. What is the greater likelihood of falling a total sum of 7 or 8? (write 7, 8, or 0 if the probabilities are the same)?
We have two dice. What is the greater likelihood of falling a total sum of 7 or 8? (write 7, 8, or 0 if the probabilities are the same)? - Std-deviation
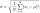 Calculate standard deviation for file: 63,65,68,69,69,72,75,76,77,79,79,80,82,83,84,88,90
Calculate standard deviation for file: 63,65,68,69,69,72,75,76,77,79,79,80,82,83,84,88,90 - VCP equation
 Solve the following equation with variations, combinations, and permutations: 4 V(2,x)-3 C(2,x+ 1) - x P(2) = 0
Solve the following equation with variations, combinations, and permutations: 4 V(2,x)-3 C(2,x+ 1) - x P(2) = 0 - RWY
 Calculate the opposite direction of the runway 13. Runways are named by a number between 01 and 36, which is generally one-tenth of the azimuth of the runway's heading in degrees: a runway numbered 09 points east (90°), runway 18 is south (180°), runway 2
Calculate the opposite direction of the runway 13. Runways are named by a number between 01 and 36, which is generally one-tenth of the azimuth of the runway's heading in degrees: a runway numbered 09 points east (90°), runway 18 is south (180°), runway 2 - Rich retirement
 Health care issues are receiving much attention in both academic and political arenas. A sociologist recently surveyed citizens over 60 years of age whose net worth is too high to qualify for government health care but who have no private health insurance
Health care issues are receiving much attention in both academic and political arenas. A sociologist recently surveyed citizens over 60 years of age whose net worth is too high to qualify for government health care but who have no private health insurance
- And or logic
 If A and B are events with P(A)=0.3, P(A OR B)=0.76, and P(A AND B)=0.04, find P(B). Enter your answer in decimal form, rounded to one place.
If A and B are events with P(A)=0.3, P(A OR B)=0.76, and P(A AND B)=0.04, find P(B). Enter your answer in decimal form, rounded to one place. - Three sigma rule
 Stomach weights are normally distributed, with a mean of 1314g and a standard deviation of 113g. State the probability that a randomly selected stomach weighs more than 1118g. (Report the probabilities using at least four decimal places. )
Stomach weights are normally distributed, with a mean of 1314g and a standard deviation of 113g. State the probability that a randomly selected stomach weighs more than 1118g. (Report the probabilities using at least four decimal places. ) - Digits
 How many odd four-digit numbers can we create from digits: 0, 3, 5, 6, and 7? (a) the figures may be repeated (b) the digits may not be repeated
How many odd four-digit numbers can we create from digits: 0, 3, 5, 6, and 7? (a) the figures may be repeated (b) the digits may not be repeated
