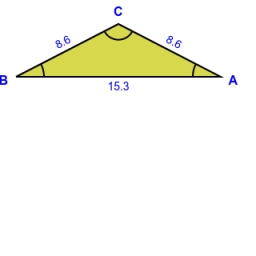
Isosceles triangle
In an isosceles triangle ABC with base AB; A [3,4]; B [1,6] and the vertex C lies on the line 5x - 6y - 16 = 0. Calculate the coordinates of vertex C.
Correct answer:
Tips for related online calculators
Are you looking for help with calculating roots of a quadratic equation?
Do you have a linear equation or system of equations and looking for its solution? Or do you have a quadratic equation?
Do you want to convert length units?
See also our right triangle calculator.
Calculation of an isosceles triangle.
See also our trigonometric triangle calculator.
Do you have a linear equation or system of equations and looking for its solution? Or do you have a quadratic equation?
Do you want to convert length units?
See also our right triangle calculator.
Calculation of an isosceles triangle.
See also our trigonometric triangle calculator.
You need to know the following knowledge to solve this word math problem:
- geometry
- analytic geometry
- algebra
- quadratic equation
- equation
- system of equations
- expression of a variable from the formula
- planimetrics
- Pythagorean theorem
- right triangle
- triangle
Units of physical quantities:
Grade of the word problem:
Related math problems and questions:
- Center
 In the ABC triangle is point D[1,-2,6], which is the center of the |BC|, and point G[8,1,-3], which is the center of gravity of the triangle. Find the coordinates of the vertex A[x,y,z].
In the ABC triangle is point D[1,-2,6], which is the center of the |BC|, and point G[8,1,-3], which is the center of gravity of the triangle. Find the coordinates of the vertex A[x,y,z]. - Square side
 Calculate the length of the side square ABCD with vertex A[0, 0] if diagonal BD lies on line p: -4x -5 =0.
Calculate the length of the side square ABCD with vertex A[0, 0] if diagonal BD lies on line p: -4x -5 =0. - X-coordinate 81737
 In triangle ABC, determine the coordinates of point B if you know that points A and B lie on the line 3x-y-5=0, points A and C lie on line 2x+3y+4=0, point C lies on the x-coordinate axis, and the angle at vertex C is right.
In triangle ABC, determine the coordinates of point B if you know that points A and B lie on the line 3x-y-5=0, points A and C lie on line 2x+3y+4=0, point C lies on the x-coordinate axis, and the angle at vertex C is right. - Chord BC
 A circle k has the center at the point S = [0; 0]. Point A = [40; 30] lies on the circle k. How long is the chord BC if the center P of this chord has the coordinates [- 14; 0]?
A circle k has the center at the point S = [0; 0]. Point A = [40; 30] lies on the circle k. How long is the chord BC if the center P of this chord has the coordinates [- 14; 0]?
- Coordinates of a centroind
 Let’s A = [3, 2, 0], B = [1, -2, 4] and C = [1, 1, 1] be 3 points in space. Calculate the coordinates of the centroid of △ABC (the intersection of the medians).
Let’s A = [3, 2, 0], B = [1, -2, 4] and C = [1, 1, 1] be 3 points in space. Calculate the coordinates of the centroid of △ABC (the intersection of the medians). - Conditions 7186
 Given an isosceles right triangle ABS with base AB. On a circle centered at point S and passing through points A and B, point C lies such that triangle ABC is isosceles. Determine how many points C satisfy the given conditions and construct all such point
Given an isosceles right triangle ABS with base AB. On a circle centered at point S and passing through points A and B, point C lies such that triangle ABC is isosceles. Determine how many points C satisfy the given conditions and construct all such point - Triangle midpoints
 Determine coordinates of triangle ABC vertices if we know triangle sides midpoints SAB [0;3] SBC [1;6] SAC [4;5], its sides AB, BC, AC.
Determine coordinates of triangle ABC vertices if we know triangle sides midpoints SAB [0;3] SBC [1;6] SAC [4;5], its sides AB, BC, AC. - Triangle IRT
 An isosceles right triangle ABC with right angle at vertex C has vertex coordinates: A (-1, 2); C (-5, -2). Calculate the length of segment AB.
An isosceles right triangle ABC with right angle at vertex C has vertex coordinates: A (-1, 2); C (-5, -2). Calculate the length of segment AB. - Calculate 8
 Calculate the coordinates of point B axially symmetrical with point A[-1, -3] along a straight line p : x + y - 2 = 0.
Calculate the coordinates of point B axially symmetrical with point A[-1, -3] along a straight line p : x + y - 2 = 0.
- Right-angled 82561
 Determine point C so that triangle ABC is right-angled and isosceles with hypotenuse AB, where A[4,-6], B[-2,10]
Determine point C so that triangle ABC is right-angled and isosceles with hypotenuse AB, where A[4,-6], B[-2,10] - Equation 2604
 The given triangle is ABC: A [-3; -1] B [5; 3] C [1; 5] Write the line equation that passes through the vertex C parallel to the side AB.
The given triangle is ABC: A [-3; -1] B [5; 3] C [1; 5] Write the line equation that passes through the vertex C parallel to the side AB. - Segment
 Calculate the segment AB's length if the coordinates of the end vertices are A[10, -4] and B[5, 5].
Calculate the segment AB's length if the coordinates of the end vertices are A[10, -4] and B[5, 5]. - Vertex of the rectangle
 Determine the coordinates of the vertex of the rectangle inscribed in the circle x²+y² -2x-4y-20=0 if you know that one of its sides lies on the line p: x+2y=0
Determine the coordinates of the vertex of the rectangle inscribed in the circle x²+y² -2x-4y-20=0 if you know that one of its sides lies on the line p: x+2y=0 - Square ABCD
 Construct a square ABCD with center S [3,2] and the side a = 4 cm. Point A lies on the x-axis. Construct a square image in the displacement given by oriented segment SS'; S` [-1 - 4].
Construct a square ABCD with center S [3,2] and the side a = 4 cm. Point A lies on the x-axis. Construct a square image in the displacement given by oriented segment SS'; S` [-1 - 4].
- Direction vector
 The line p is given by the point P [- 0,5; 1] and the direction vector s = (1,5; - 3) determines: A) value of parameter t for points X [- 1,5; 3], Y [1; - 2] lines p B) whether the points R [0,5; - 1], S [1,5; 3] lies on the line p C) parametric equations
The line p is given by the point P [- 0,5; 1] and the direction vector s = (1,5; - 3) determines: A) value of parameter t for points X [- 1,5; 3], Y [1; - 2] lines p B) whether the points R [0,5; - 1], S [1,5; 3] lies on the line p C) parametric equations - Circle
 The circle k with diameter |MN| = 61. Point J lies on the circle k. Line |MJ|=22. Calculate the length of a segment JN.
The circle k with diameter |MN| = 61. Point J lies on the circle k. Line |MJ|=22. Calculate the length of a segment JN. - Calculate 82578
 The vertices of triangle ABC are: A[1, 2, -3], B[0, 1, 2], C[2, 1, 1]. Calculate the lengths of sides AB, AC and the angle at vertex A.
The vertices of triangle ABC are: A[1, 2, -3], B[0, 1, 2], C[2, 1, 1]. Calculate the lengths of sides AB, AC and the angle at vertex A.
