V rovnoramenném trojúhelníku
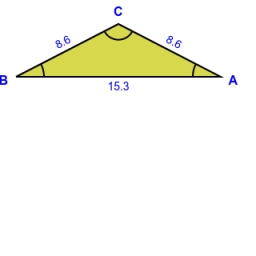
V rovnoramenném trojúhelníku ABC se základnou AB; A [-3,4]; B [1,6] leží vrchol C na přímce 5x - 6y - 16 = 0. Vypočítejte souřadnice vrcholu C.
Vaše odpověď:
Vaše odpověď:
Zobrazuji 2 komentáře:
Sisi
Dobrý den, můžete mě prosím navést z čeho vychází vzoreček použitý k výpočtu (x−xo)² + (y−yo)² = (x−x1)² + (y−y1)². Pravděpodobně mi uniká nějaká předchozí látka, a tak nechápu, proč ho použit.
Matik
Pythagorova veta... delky dvou usecek se rovnaji ... rovnaji se take delky jejich ctvercu:
c2 = a2+b2 = x2+y2
c2 = a2+b2 = x2+y2
Tipy na související online kalkulačky
Hledáte pomoc s výpočtem kořenů kvadratické rovnice?
Máte lineární rovnici nebo soustavu rovnic a hledáte její řešení? Nebo máte kvadratickou rovnici?
Chcete proměnit jednotku délky?
Vyzkoušejte také naši kalkulačku pravouhlého trojuholníka.
Vypočet rovnoramenného trojúhelníku.
Vyzkoušejte také naši trigonometrickou trojúhelníkovou kalkulačku.
Máte lineární rovnici nebo soustavu rovnic a hledáte její řešení? Nebo máte kvadratickou rovnici?
Chcete proměnit jednotku délky?
Vyzkoušejte také naši kalkulačku pravouhlého trojuholníka.
Vypočet rovnoramenného trojúhelníku.
Vyzkoušejte také naši trigonometrickou trojúhelníkovou kalkulačku.
K vyřešení této úlohy jsou potřebné tyto znalosti z matematiky:
geometriealgebraplanimetrieJednotky fyzikálních veličinÚroveň náročnosti úkolu
Doporučujeme k tomuto príkladu si prohlédnout toto výukové video: video1
Související a podobné příklady:
- Těžiště
V trojúhelníku ABC leží bod D[1,-2,6], který je středem strany |BC| a bod G, který je těžištěm trojúhelníku G[8,1,-3]. Najděte souřadnice vrcholu A[x,y,z]. - Vrcholy trojúhelníku
Určete souřadnice vrcholu trojúhelníku ABC, známe-li středy SAB [0;3] SBC [1;6] SAC [4;5], jeho stran AB, BC, AC. - Souřadnice bodu B
V trojúhelníku ABC určete souřadnice bodu B, pokud víte, že body A, B leží na přímce 3x-y-5=0, body A, C leží na přímce 2x+3y+4=0, bod C leží na souřadnicové ose x a úhel u vrcholu C je pravý. - Strana
Vypočítejte velikost strany čtverce ABCD s vrcholem A [0, 0], pokud úhlopříčka BD leží na přímce p: -4x -5 =0. - Rovnoramenný - osy uhlov
V rovnoramenném trojúhelníku ABC se základnou AB platí ∠BAC = 20°, AB = 4. Osa vnitřního úhlu u vrcholu B protíná stranu AC v bodě P. Vypočítejte délku úsečky AP. Výsledek uveďte s přesností na dvě desetinná místa. - Strany a úhel trojúhelníku ABC
Vrcholy trojúhelníku ABC jsou: A[1, 2, -3], B[0, 1, 2], C[2, 1, 1]. Vypočítejte délky stran AB, AC a úhel při vrcholu A. - Obsah Č.T.
Je dán čtverec EQBO, přičemž |QB|=24. Vypočítejte obsah trojúhelníku EOA, kde vrchol A leží na přímce BQ.
