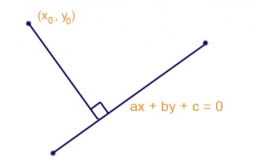
Equation of the circle
Find the equation of the circle with the center at (1,20), which touches the line 8x+5y-19=0
Correct answer:
Showing 1 comment:
Dr Math
Hint - use formula for Distance Between a Point and a Line = which is radius of circle
5 years ago 3 Likes
Tips for related online calculators
Need help calculating sum, simplifying, or multiplying fractions? Try our fraction calculator.
Our vector sum calculator can add two vectors given by their magnitudes and by included angle.
See also our right triangle calculator.
See also our trigonometric triangle calculator.
Our vector sum calculator can add two vectors given by their magnitudes and by included angle.
See also our right triangle calculator.
See also our trigonometric triangle calculator.
You need to know the following knowledge to solve this word math problem:
Related math problems and questions:
- Crosswind
 A plane is traveling 45 degrees N of E at 320 km/h when it comes across a current from S of E at 115 degrees of 20 km/h. What are the airplane's new course and speed?
A plane is traveling 45 degrees N of E at 320 km/h when it comes across a current from S of E at 115 degrees of 20 km/h. What are the airplane's new course and speed? - Vectors
 Find the magnitude of the angle between two vectors u = (3; -5) and v = (10; 6)
Find the magnitude of the angle between two vectors u = (3; -5) and v = (10; 6) - Space vectors 3D
 The vectors u = (1; 3; -4), v = (0; 1; 1) are given. Find the size of these vectors, calculate the angle of the vectors, and the distance between the vectors.
The vectors u = (1; 3; -4), v = (0; 1; 1) are given. Find the size of these vectors, calculate the angle of the vectors, and the distance between the vectors. - Vectors abs sum diff
 The vectors a = (4,2), b = (- 2,1) are given. Calculate: a) |a+b|, b) |a|+|b|, c) |a-b|, d) |a|-|b|.
The vectors a = (4,2), b = (- 2,1) are given. Calculate: a) |a+b|, b) |a|+|b|, c) |a-b|, d) |a|-|b|.
- Calculate 6
 Calculate the distance of point A[0, 2] from a line passing through points B[9, 5] and C[1, -1].
Calculate the distance of point A[0, 2] from a line passing through points B[9, 5] and C[1, -1]. - The modulus
 Find the modulus of the complex number 2 + 5i
Find the modulus of the complex number 2 + 5i - Angle of the body diagonals
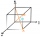 Using the vector dot product calculate the angle of the body diagonals of the cube.
Using the vector dot product calculate the angle of the body diagonals of the cube. - Coordinates of square vertices
 The ABCD square has the center S [−3, −2] and the vertex A [1, −3]. Find the coordinates of the other vertices of the square.
The ABCD square has the center S [−3, −2] and the vertex A [1, −3]. Find the coordinates of the other vertices of the square. - Rectangle 39
 Find the perimeter and area of the rectangular with vertices (-1, 4), (0,4), (0, -1), and (-4, 4)
Find the perimeter and area of the rectangular with vertices (-1, 4), (0,4), (0, -1), and (-4, 4)
- Airplane navigation
 An airplane leaves an airport and flies west 120 miles and then 150 miles in the direction S 44.1°W. How far is the plane from the airport (round to the nearest mile)?
An airplane leaves an airport and flies west 120 miles and then 150 miles in the direction S 44.1°W. How far is the plane from the airport (round to the nearest mile)? - Add vector
 Given that P = (5, 8) and Q = (6, 9), find the component form and magnitude of vector PQ.
Given that P = (5, 8) and Q = (6, 9), find the component form and magnitude of vector PQ. - 3d vector component
 The vector u = (3.9, u3), and the length of the vector u is 12. What is, is u3?
The vector u = (3.9, u3), and the length of the vector u is 12. What is, is u3? - Vectors
 Vector a has coordinates (8; 10), and vector b has coordinates (0; 17). If the vector c = b - a, what is the magnitude of the vector c?
Vector a has coordinates (8; 10), and vector b has coordinates (0; 17). If the vector c = b - a, what is the magnitude of the vector c? - Unit vector 2D
 Find coordinates of unit vector to vector AB if A[-6; 8], B[-18; 10].
Find coordinates of unit vector to vector AB if A[-6; 8], B[-18; 10].
- Triangle
 Plane coordinates of vertices: K[19, -4] L[9, 13] M[-20, 8] give Triangle KLM. Calculate its area and its interior angles.
Plane coordinates of vertices: K[19, -4] L[9, 13] M[-20, 8] give Triangle KLM. Calculate its area and its interior angles. - Vector
 Calculate the length of the vector v&; 8407; = (9.75, 6.75, -6.5, -3.75, 2).
Calculate the length of the vector v&; 8407; = (9.75, 6.75, -6.5, -3.75, 2). - Square
 Points A[9,9] and B[-4,1] are adjacent vertices of the square ABCD. Calculate the area of the square ABCD.
Points A[9,9] and B[-4,1] are adjacent vertices of the square ABCD. Calculate the area of the square ABCD.
