Kružnice a tečna
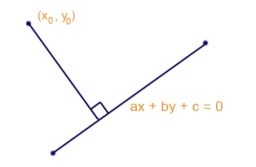
Najděte rovnici kružnice se středem v (1,20), která se dotýká přímky 8x + 5y-19 = 0
Vaše odpověď:
Vaše odpověď:
Tipy na související online kalkulačky
Dva vektory určeny velikostmi a vzájemným úhlem sčítá naše kalkulačka sčítání vektorů .
Vyzkoušejte také naši kalkulačku pravouhlého trojuholníka.
Vyzkoušejte také naši trigonometrickou trojúhelníkovou kalkulačku.
Vyzkoušejte také naši kalkulačku pravouhlého trojuholníka.
Vyzkoušejte také naši trigonometrickou trojúhelníkovou kalkulačku.
K vyřešení této úlohy jsou potřebné tyto znalosti z matematiky:
geometriealgebraaritmetikaplanimetrie
Doporučujeme k tomuto príkladu si prohlédnout toto výukové video: video1
Související a podobné příklady:
- Kružnice
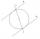Kružnice se dotýká dvou rovnoběžek p a q, její střed leží na přímce a, která je sečnou obou přímek. Napište její rovnici a určete souřadnice středu a poloměru. p: -5x-y-1 = 0 q: -5x-y+7 = 0 a: -2x+5y-6 = 0 - Kružnice
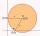Napište rovnici kružnice která procházi bodem [0,6] a dotýka se osy x v bode [5,0]: (x-x_S)²+(y-y_S)²=r² - Rovnoběžná přímka bodem
Najděte rovnici přímky, která prochází přes bod (1, 3) a je rovnoběžná s přímkou y = - 2x + 4. - Kružnice
Dokažte, že rovnice k1 a k2 představují kružnice. Napište rovnici přímky, která prochází středy těchto kružnic. k1: x²+y²+2x+4y+1=0 k2: x²+y²-8x+6y+9=0 - Rovnice kruhu
Najděte rovnici kruhu se středem (3,7) a obvodem 8π jednotek. - Přímka
Napište rovnici přímky rovnoběžné s 9x + 3y = 8, která prochází bodem (-1, -4). Napište ve tvaru ax + by = c. - Rovnice kružnice
Najděte rovnici kružnice, která se dotýká osy y ve vzdálenosti 4 od počátku a vysekne tětivu délky 6 na ose x.
