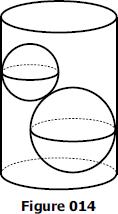
Two balls
Two balls, one 8cm in radius and the other 6cm in radius, are placed in a cylindrical plastic container 10cm in radius. Find the volume of water necessary to cover them.
Correct answer:
Tips for related online calculators
Need help calculating sum, simplifying, or multiplying fractions? Try our fraction calculator.
Tip: Our volume units converter will help you convert volume units.
See also our right triangle calculator.
See also our trigonometric triangle calculator.
Tip: Our volume units converter will help you convert volume units.
See also our right triangle calculator.
See also our trigonometric triangle calculator.
You need to know the following knowledge to solve this word math problem:
- arithmetic
- square root
- solid geometry
- cylinder
- sphere
- space diagonal
- planimetrics
- Pythagorean theorem
- right triangle
- triangle
- diagonal
- numbers
- fractions
Units of physical quantities:
Grade of the word problem:
Related math problems and questions:
- Cube in sphere
 The cube is inscribed in a sphere with a radius r = 6 cm. What percentage is the cube's volume from the ball's volume?
The cube is inscribed in a sphere with a radius r = 6 cm. What percentage is the cube's volume from the ball's volume? - Tangent spheres
 A sphere with a radius of 1 m is placed in the corner of the room. What is the largest sphere size that fits into the corner behind it? Additional info: Two spheres are placed in the corner of a room. The spheres are each tangent to the walls and floor an
A sphere with a radius of 1 m is placed in the corner of the room. What is the largest sphere size that fits into the corner behind it? Additional info: Two spheres are placed in the corner of a room. The spheres are each tangent to the walls and floor an - Cube into sphere
 The cube has brushed a sphere as large as possible. Determine how much percent the waste was.
The cube has brushed a sphere as large as possible. Determine how much percent the waste was. - Cube in sphere
 The sphere is an inscribed cube with an edge of 8 cm. Find the sphere's radius.
The sphere is an inscribed cube with an edge of 8 cm. Find the sphere's radius.
- Cube and sphere
 A cube with a surface area of 150 cm² is described sphere. What is a sphere surface?
A cube with a surface area of 150 cm² is described sphere. What is a sphere surface? - Billiard balls
 A layer of ivory billiard balls radius of 6.35 cm is in the form of a square. The balls are arranged so that each ball is tangent to everyone adjacent to it. In the spaces between sets of 4 adjacent balls, other balls rest, equal in size to the original.
A layer of ivory billiard balls radius of 6.35 cm is in the form of a square. The balls are arranged so that each ball is tangent to everyone adjacent to it. In the spaces between sets of 4 adjacent balls, other balls rest, equal in size to the original. - Sphere vs cube
 How much % of the surface of a sphere of radius 12 cm is the surface of a cube inscribed in this sphere?
How much % of the surface of a sphere of radius 12 cm is the surface of a cube inscribed in this sphere? - Sphere area
 A cube with an edge 1 m long is a circumscribed sphere (vertices of the cube lie on a sphere's surface). Find the surface area of the sphere.
A cube with an edge 1 m long is a circumscribed sphere (vertices of the cube lie on a sphere's surface). Find the surface area of the sphere. - Sphere and cone
 Within the sphere of radius G = 33 cm, inscribe the cone with the largest volume. What is that volume, and what are the dimensions of the cone?
Within the sphere of radius G = 33 cm, inscribe the cone with the largest volume. What is that volume, and what are the dimensions of the cone?
- Cube in a sphere
 The cube is inscribed in a sphere with a volume 7253 cm³. Determine the length of the edges of a cube.
The cube is inscribed in a sphere with a volume 7253 cm³. Determine the length of the edges of a cube. - Cubes
 One cube is an inscribed sphere, and the other one is described. Calculate the difference of volumes of cubes if the difference of surfaces in 231 cm².
One cube is an inscribed sphere, and the other one is described. Calculate the difference of volumes of cubes if the difference of surfaces in 231 cm². - Cube in ball
 The cube is inscribed into the sphere of radius 181 dm. How many percent is the volume of cube of the volume of the sphere?
The cube is inscribed into the sphere of radius 181 dm. How many percent is the volume of cube of the volume of the sphere? - Calculate 415
 Calculate the cuboid's dimensions if the sum of its edges is 19cm. The body's diagonal size is 13 cm, and its volume is 144 cm³. The total surface area is 192 cm².
Calculate the cuboid's dimensions if the sum of its edges is 19cm. The body's diagonal size is 13 cm, and its volume is 144 cm³. The total surface area is 192 cm². - Tent - spherical cap
 I have a tent in the shape of a spherical cap. Assume we want the volume to be 4 cubic meters, to sleep two or three people. Assume that the material making up the dome of the ten is twice as expensive per square as the material touching the ground. What
I have a tent in the shape of a spherical cap. Assume we want the volume to be 4 cubic meters, to sleep two or three people. Assume that the material making up the dome of the ten is twice as expensive per square as the material touching the ground. What
- Helium balloon
 Oscar needs to fill a sphere-shaped balloon with helium. If the balloon has a diameter of 8 inches, what is the total amount of helium that the balloon will hold to the nearest tenth?
Oscar needs to fill a sphere-shaped balloon with helium. If the balloon has a diameter of 8 inches, what is the total amount of helium that the balloon will hold to the nearest tenth? - Portioning ice cream
 How many scoops of ice cream can we make using a scoop in the shape of a spherical canopy with a radius of 2.5 cm and a height of 4 cm. We have a 2-liter ice cream tub available. When portioning, we will follow the exact measure.
How many scoops of ice cream can we make using a scoop in the shape of a spherical canopy with a radius of 2.5 cm and a height of 4 cm. We have a 2-liter ice cream tub available. When portioning, we will follow the exact measure. - Iron ball 2
 What is the mass of the iron ball with a diameter of 1,0 dm? The density of iron is 7870 kg/m³. .
What is the mass of the iron ball with a diameter of 1,0 dm? The density of iron is 7870 kg/m³. .
