Planimetrics - math word problems - page 100 of 185
Number of problems found: 3687
- Minute hand distance
 The distance between the tip of the minute hand and the center of the dial is 12 mm. Determine the distance traveled by the tip in 45 min. (draw a clock face and a minute hand and realize the distance it will cover in 45 min.)
The distance between the tip of the minute hand and the center of the dial is 12 mm. Determine the distance traveled by the tip in 45 min. (draw a clock face and a minute hand and realize the distance it will cover in 45 min.) - Building shadow height
 The school building casts a shadow 16 m long on the plane of the yard, and at the same time, a vertical meter pole casts a shadow 132 cm long. Determine the height of the building.
The school building casts a shadow 16 m long on the plane of the yard, and at the same time, a vertical meter pole casts a shadow 132 cm long. Determine the height of the building. - Hairs
 Suppose the length of the hair is affected by only the α-keratin synthesis, which is the major component. This synthesis takes place in the epithelial cells of the hair bulb. The structure of α-keratin is made up of α-helix for the 3.6 amino acid residues
Suppose the length of the hair is affected by only the α-keratin synthesis, which is the major component. This synthesis takes place in the epithelial cells of the hair bulb. The structure of α-keratin is made up of α-helix for the 3.6 amino acid residues - The amphitheater
 The amphitheater has the shape of a semicircle, the spectators sit on the perimeter of the semicircle, and the stage forms the diameter of the semicircle. Which spectators, P, Q, R, S, and T, see the stage at the greatest viewing angle?
The amphitheater has the shape of a semicircle, the spectators sit on the perimeter of the semicircle, and the stage forms the diameter of the semicircle. Which spectators, P, Q, R, S, and T, see the stage at the greatest viewing angle? - Calculate 8
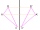 Calculate the coordinates of point B axially symmetrical with point A[-1, -3] along a straight line p : x + y - 2 = 0.
Calculate the coordinates of point B axially symmetrical with point A[-1, -3] along a straight line p : x + y - 2 = 0. - Triangle similarity
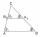 Find out if the triangles ABC and A'B'C' are similar, determine the similarity coefficient and write the similarity: a = 40 mm, b = 48 mm, c = 32 mm a´ = 60 mm, b´ = 50 mm, c´ = 40 mm
Find out if the triangles ABC and A'B'C' are similar, determine the similarity coefficient and write the similarity: a = 40 mm, b = 48 mm, c = 32 mm a´ = 60 mm, b´ = 50 mm, c´ = 40 mm - Similar Triangles Angle Sum
 Triangles ABC and A'B'C'. They are similar. In triangle ABC, the measures of the two angles are 25 degrees and 65 degrees. Explain why, in triangle A'B'C', the sum of the sizes of the two angles is equal to 90 degrees.
Triangles ABC and A'B'C'. They are similar. In triangle ABC, the measures of the two angles are 25 degrees and 65 degrees. Explain why, in triangle A'B'C', the sum of the sizes of the two angles is equal to 90 degrees. - Touch circle
 Point A has a distance (A, k) = 10 cm from a circle k with radius r = 4 cm and center S. Calculate: a) the distance of point A from the point of contact T if the tangent to the circle is drawn from point A b) the distance of the contact point T from the l
Point A has a distance (A, k) = 10 cm from a circle k with radius r = 4 cm and center S. Calculate: a) the distance of point A from the point of contact T if the tangent to the circle is drawn from point A b) the distance of the contact point T from the l - The coordinates
 The coordinates (5, 2) and (-6, 2) are vertices of a hexagon. Explain how to find the length of the segment formed by these endpoints. How long is the segment?
The coordinates (5, 2) and (-6, 2) are vertices of a hexagon. Explain how to find the length of the segment formed by these endpoints. How long is the segment? - The chord
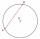 A chord passing through its center is the side of the triangle inscribed in a circle. What size are a triangle's internal angles if one is 40°?
A chord passing through its center is the side of the triangle inscribed in a circle. What size are a triangle's internal angles if one is 40°? - Viewing Two Poles
 Two straight paths cross, making an angle alpha = 53 degrees 30'. There are two pillars on one of them, one at the intersection, the other at a distance of 500m from it. How far does one have to go from the intersection along the other road to see both po
Two straight paths cross, making an angle alpha = 53 degrees 30'. There are two pillars on one of them, one at the intersection, the other at a distance of 500m from it. How far does one have to go from the intersection along the other road to see both po - Point distance shape
 What geometric shape do all points in the plane have the same distance from a given point in the plane?
What geometric shape do all points in the plane have the same distance from a given point in the plane? - Circle radius calculation
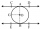 Point B is the center of the circle. The line AC touches the circles at point C and applies AB = 20 cm and AC = 16 cm. What is the radius of the circle BC?
Point B is the center of the circle. The line AC touches the circles at point C and applies AB = 20 cm and AC = 16 cm. What is the radius of the circle BC? - Theater podium angle
 The theater has the shape of a semicircle, and the podium is the diameter of a semicircle. Spectators K, L, M, N, and O, sit around the perimeter. Who sees the podium at the greatest angle?
The theater has the shape of a semicircle, and the podium is the diameter of a semicircle. Spectators K, L, M, N, and O, sit around the perimeter. Who sees the podium at the greatest angle? - Triangle congruent sides
 The perimeter of triangle MAK is 216 mm, side a = 81 mm, and side k = 62 mm. Determine the side length of the triangle OSA if the triangle MAK is congruent to the triangle OSA.
The perimeter of triangle MAK is 216 mm, side a = 81 mm, and side k = 62 mm. Determine the side length of the triangle OSA if the triangle MAK is congruent to the triangle OSA. - Three points
 Three points, K (-3; 2), L (-1; 4), and M (3, -4), are given. Find out: (a) whether the triangle KLM is right b) calculate the length of the line to the k side c) write the coordinates of the vector LM d) write the directional form of the KM side e) write
Three points, K (-3; 2), L (-1; 4), and M (3, -4), are given. Find out: (a) whether the triangle KLM is right b) calculate the length of the line to the k side c) write the coordinates of the vector LM d) write the directional form of the KM side e) write - Isosceles triangle perimeter
 Two isosceles triangles have the same angle at the vertex opposite the base. The first one has a base of 12 cm and a leg of 9 cm. The other has a 16 cm long base. Calculate the perimeter of the second triangle.
Two isosceles triangles have the same angle at the vertex opposite the base. The first one has a base of 12 cm and a leg of 9 cm. The other has a 16 cm long base. Calculate the perimeter of the second triangle. - Circle distance
 For circles k1 (S1, 4cm) and k2 (S2, 3cm) and it holds that | S1S2 | = 8cm. Determine the distance between the circles K1 and K2.
For circles k1 (S1, 4cm) and k2 (S2, 3cm) and it holds that | S1S2 | = 8cm. Determine the distance between the circles K1 and K2. - Similar triangles
 We have similar triangles ABC with angle CAB=45° and angle ACB= 30° and a similar triangle OPN. What is the angle NOP in a similar triangle?
We have similar triangles ABC with angle CAB=45° and angle ACB= 30° and a similar triangle OPN. What is the angle NOP in a similar triangle? - Clock face
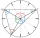 On the circular face of the clock, we connect the points corresponding to the numbers 2, 5, and 9 to each other, which creates a triangle. Calculate the sizes of all interior angles.
On the circular face of the clock, we connect the points corresponding to the numbers 2, 5, and 9 to each other, which creates a triangle. Calculate the sizes of all interior angles.
Do you have homework that you need help solving? Ask a question, and we will try to solve it. Solving math problems.
