Planimetrics - math word problems - page 103 of 184
Number of problems found: 3667
- Circle from string
Martin has a long 628 mm string. He makes a circle from it. Calculate the radius of the circle. - Reverse Pythagorean theorem
Given are the lengths of the sides of the triangles. Decide which one is rectangular: Δ ABC: 66 dm, 60 dm, 23 dm ... Δ DEF: 20 mm, 15 mm, 25 mm ... Δ GHI: 16 cm, 20 cm, 12 cm ... Δ JKL: 58 cm, 63 cm, 23 cm ... Δ MNO: 115 mm, - Triangle 15123
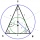In triangle ABC, we know the angle BAC = 50 degrees. What is the angle between the axis of the angle ACB and the axis of the angle CAB? - Quadrangular 4559
The quadrangular garden should be fenced off with a slatted fence. The sides of the orchard are 65m, 78m, 40m and 32m. The wheels are to be placed 6m apart, and the axes of the rims are 15cm apart. How much is needed for a wheel fence, and how many batten - The plot
Mr. Duma recently inherited a rectangular plot, part of the estate left by his late father. The plot with the following dimensions: Length=2x+1; Width=x-1. Determine the formula, in terms of x, that best describes the area of the rectangular plot. He has - Circumference 7143
Peter drew a regular hexagon, the vertices of which lay on a circle 16 cm long. Then, for each vertex of this hexagon, he drew a circle centered on that vertex that ran through its two adjacent vertices. The unit was created as in the picture. Find the ci - Angles
In the triangle ABC, the ratio of angles is α:β = 4:5. The angle γ is 36°. How big are the angles α and β? - Circle arc
The circle segment has a circumference of 135.26 dm and 2096.58 dm² area. Calculate the radius of the circle and the size of the central angle. - Calculate 7214
Two tangents are drawn from point C to a circle with a radius of 76 mm. The distance between the two contact points is 14 mm. Calculate the distance of point C from the center of the circle. - Natural fertilizer
The gardener fertilized the rectangular garden measuring 120m and 60m with 16kg of natural fertilizer. Natural fertilizer contains 45% organic matter. How much organic matter falls on 1 m² of the garden? - Area of iso-trap
Find the area of an isosceles trapezoid if the lengths of its bases are 16 cm and 30 cm and the diagonals are perpendicular to each other. - Circumference 64104
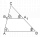The ABC triangle has a circumference of 11 cm. Triangle A'B'C ', similar to triangle ABC, has side lengths of 6 cm, 120 mm, and 1.5 dm larger than triangle ABC. Calculate the area of the triangle A'B'C '. - Circle - AG
Find the coordinates of the circle and its diameter if its equation is: x² + y² - 6x-4y=36 - Medians in triangle
The median of the isosceles triangle is 3 cm long. If its perimeter is 16 cm, determine the size of its sides. - Distance 6164
What is the area of a square when the distance between parallel lines is 6? - Strawberries 82738
Three classmates worked part-time during the summer vacation harvesting strawberries. Jan collected 145 baskets of strawberries during the entire brigade. Peter collected 185 baskets. How many baskets did their classmate Stan collect if we know that the b - Chickens and rabbits
In the yard were chickens and rabbits. Together they had 30 heads and 100 legs. How many chickens and how many rabbits were in the yard? - Equation of a circle
Write the general equation of a circle with center S(2;5) and point B(5;6) lying on this circle. - Same area
There is a given triangle. Construct a square of the same area. - Vector 7
Given vector OA(12,16) and vector OB(4,1). Find vector AB and vector |A|.
Do you have unsolved math question and you need help? Ask a question, and we will try to solve it. We solve math question.
