Planimetrics - math word problems - page 145 of 185
Number of problems found: 3685
- The straight
The straight path rises by 72 cm every 3 m of its length. How many meters will it climb to 350 m? - Tree shadow
The shadow of the tree is 16 meters long. The shadow of a two-meter-high tourist sign beside standing is 3.2 meters long. What height is a tree (in meters)? - Circumference 42471
The lengths of the sides of the triangle ABC are in the ratio 4:2:5. Calculate the size of the longest side of a similar KLM triangle, whose circumference is 66 cm. - Exterior angles
In triangle ABC, the size of the exterior angle at vertex C is equal to 126°. The size of the internal angles at vertices A and B are in the ratio 5: 9. Calculate the size of the internal angles α, β, γ of triangle ABC. - Similar triangles
The triangles ABC and XYZ are similar. Find the unknown lengths of the sides of the triangles. a) a = 5 cm b = 8 cm x = 7.5 cm z = 9 cm b) a = 9 cm c = 12 cm y = 10 cm z = 8 cm c) b = 4 cm c = 8 cm x = 4.5 cm z = 6 cm - Candy - MO
Gretel deploys different numbers to the vertex of a regular octagon, from one to eight candy. Peter can then choose which three piles of candy to give Gretel others retain. The only requirement is that the three piles lie at the vertices of an isosceles t - Vertical 29801
The shadow of the building is 16 m long, and the shadow of the vertical meter rod is 0.8 m long at the same time. What is the height of the building? - Circumference 4246
In the ABC triangle, we connected the centers of the sides, creating a smaller triangle with a circumference of 14 centimeters. What is the perimeter of triangle ABC? - Axial symmetry
Find the image A' of point A [1,2] in axial symmetry with the axis p: x = -1 + 3t, y = -2 + t (t = are a real number) - Express the unknown
Calculate the unknown from the formula p=F: S Express the unknown F - Similarity of two triangles
The KLM triangle has a side length of k = 6.3cm, l = 8.1cm, m = 11.1cm. The triangle XYZ has a side length of x = 8.4cm, y = 10.8cm, z = 14.8cm. Are triangle KLM and XYZ similar? (write 0. If not, if yes, find and write the coefficient of a similarity) - The shadow
The shadow of a 1 m high pole thrown on a horizontal plane is 0.8 m long. At the same time, the shadow of a tree thrown on a horizontal plane is 6.4 m. Determine the height of the tree. - Rhombus MATH
Construct a rhombus M A T H with diagonal MT=4cm, angle MAT=120° - Three parallels
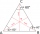The vertices of an equilateral triangle lie on three different parallel lines. The middle line is 5 m and 3 m distant from the end lines. Calculate the height of this triangle. - Circle described
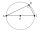The circle radius described in the right triangle with a 6 cm long leg is 5 cm. Calculate the circumference of this triangle. - Reconstruction of the corridor
Calculate how many minutes will be reduced to travel a 213 km long railway corridor, where the maximum speed increases from 120 km/h to 160 km/h. Calculate how many minutes will shorten travel time if we consider that the train must stop at 6 stations. Ea - Triangle 69144
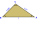The line p passes through the center of gravity T of the triangle and is parallel to the line BC. What is the ratio of the area of the divided smaller part of the triangle by the line p? What is the area of the triangle? - Observatories A,B
The target C is observed from two artillery observatories, A and B, 296 m apart. At the same time, angle BAC = 52°42" and angle ABC = 44°56". Calculate the distance of the target C from observatory A. - Right-angled triangle The right-angled triangle XYZ is similar to the triangle ABC, which has a right angle at the vertex X. The following applies: side a = 9 cm, x=4 cm, x = v-4 (v = height of triangle ABC). Calculate the unknown side lengths of both triangles.
- Two people
Two straight lines cross at right angles. Two people start simultaneously at the point of intersection. John walks at the rate of 4 kph on one road, and Jenelyn walks at the rate of 8 kph on the other road. How long will it take for them to be 20√5 km apa
Do you have unsolved math question and you need help? Ask a question, and we will try to solve it. We solve math question.
