Planimetrics - math word problems - page 144 of 185
Number of problems found: 3688
- Linden shadow height
The length of the linden shadow is 429 cm. The length of the shadow meter is 78cm. Calculate the height of the linden. - Vertical rod
The vertical one-meter-long rod casts a shadow 150 cm long. Calculate the height of a column whose shadow is 36 m long simultaneously. - Calculate
Calculate the height of a tree that casts a shadow 22 m long if you know that at the same time, a pillar 2 m high casts a shadow 3 meters long. - Shadow - an observation tower
How tall is the observation tower if it casts a shadow 9.6 m long at exactly the same moment that a half-meter pole casts a shadow 30 cm long? - Triangle arm
Two isosceles triangles have the same angle at the apex concerning the base. One has a 17 cm long arm and a 10 cm long base. The second has a base length of 8 cm. Determine the length of his arm. - Trapezoid - intersection of diagonals
In the ABCD trapezoid is AB = 8 cm long, trapezium height 6 cm, and distance of diagonals intersection from AB is 4 cm. Calculate the trapezoid area. - Triangle
Prove whether you can construct a triangle ABC if a=8 cm, b=6 cm, c=10 cm. - Largest possible area
A right-angled triangle was inscribed in a circle with a diameter of 20 cm, whose hypotenuse is the circle's diameter and has the largest possible area. Calculate the area of this triangle. - Quadrilateral in circle
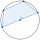A quadrilateral is inscribed in the circle. Its vertices divide the circle in a ratio of 1:2:3:4. Find the sizes of its interior angles. - Vertex of the rectangle
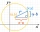Determine the coordinates of the vertex of the rectangle inscribed in the circle x²+y² -2x-4y-20=0 if you know that one of its sides lies on the line p: x+2y=0 - Sides ratio
Calculate the circumference of a triangle with an area of 84 cm² if a:b:c = 10:17:21 - Field map scale
The map shows a square-shaped field with a side length of 0.7 cm. Its area is 49 ha. Find the scale of the map. - Angles in a triangle
The angles of the triangle ABC make an arithmetic sequence with the largest angle γ=100°. What sizes have other angles in a triangle? - Tree shadow
The shadow of the tree is 16 meters long. The shadow of a two-meter-high tourist sign beside standing is 3.2 meters long. What height is a tree (in meters)? - Exterior angles
In triangle ABC, the size of the exterior angle at vertex C is equal to 126°. The size of the internal angles at vertices A and B are in the ratio 5: 9. Calculate the size of the internal angles α, β, γ of triangle ABC. - Tree shadow
The tree perpendicular to the horizontal surface has a shadow 8.32 meters long. At the same time, a one-meter rod perpendicular to the horizontal surface has a shadow 64 cm long. How tall is the tree? - Triangle perimeter
In the ABC triangle, we connected the centers of the sides, creating a smaller triangle with a circumference of 14 centimeters. What is the perimeter of triangle ABC? - The straight
The straight path rises by 72 cm every 3 m of its length. How many meters will it climb to 350 m? - Polygon 3 Polygon ABCD is dilated, rotated, and translated to form polygon QWER. The endpoints A and B are at (0, -7) and (8, 8), and the endpoints QW are at (6, -6) and (2, 1.5). What is the scale factor of the dilation?
- Express the unknown
Calculate the unknown from the formula p=F: S Express the unknown F
Do you have homework that you need help solving? Ask a question, and we will try to solve it. Solving math problems.
