Planimetrics - math word problems - page 146 of 185
Number of problems found: 3685
- 2d shape
 Calculate the area of a shape in which an arbitrary point is not more than 3 cm from the segment AB. The length of segment AB is 5 cm.
Calculate the area of a shape in which an arbitrary point is not more than 3 cm from the segment AB. The length of segment AB is 5 cm. - Hexagon
 There is a regular hexagon ABCDEF. If the area of the triangle ABC is 10, what is the area of the hexagon ABCDEF? I do not know how to solve it simply....
There is a regular hexagon ABCDEF. If the area of the triangle ABC is 10, what is the area of the hexagon ABCDEF? I do not know how to solve it simply.... - Railways
 Railways climb 2.8 ‰. Calculate the height difference between two points on the railway distant 5997 meters.
Railways climb 2.8 ‰. Calculate the height difference between two points on the railway distant 5997 meters. - Perpendicular 7001
 We throw a ball in an express car traveling at a constant speed of 24 m/s, whose initial speed relative to the vehicle is 7 m/s. What is the initial velocity of the ball relative to the surface of the ground if we throw it a) in the direction of travel b)
We throw a ball in an express car traveling at a constant speed of 24 m/s, whose initial speed relative to the vehicle is 7 m/s. What is the initial velocity of the ball relative to the surface of the ground if we throw it a) in the direction of travel b) - Millimeters 4811
 Construct a triangle ABC if you know the lengths of its sides c = 5 cm, a = 4 cm and angle ABC is 60°. Measure the length of side b in millimeters. Side length b is: a, 75 mm < b < 81 mm b, 53 mm < b < 59 mm c, 43 mm < b < 49 mm d, 13 mm
Construct a triangle ABC if you know the lengths of its sides c = 5 cm, a = 4 cm and angle ABC is 60°. Measure the length of side b in millimeters. Side length b is: a, 75 mm < b < 81 mm b, 53 mm < b < 59 mm c, 43 mm < b < 49 mm d, 13 mm - Calculate 6539
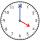 Calculate the magnitude of the angle formed by the lines p and q, which connect 1, 6 (line p), and 5, 8 (line q) on the clock face.
Calculate the magnitude of the angle formed by the lines p and q, which connect 1, 6 (line p), and 5, 8 (line q) on the clock face. - Dodecagon
 Calculate the size of the smaller angles determined by lines A1 A4 and A2 A10 in the regular dodecagon A1A2A3. .. A12. Express the result in degrees.
Calculate the size of the smaller angles determined by lines A1 A4 and A2 A10 in the regular dodecagon A1A2A3. .. A12. Express the result in degrees. - Mrak - cloud
 It is given segment AB, which is 12 cm in length, on which one side of the square MRAK is laid. MRAK's side length is 2 cm shown. MRAK gradually flips along the line segment AB, and point R leaves a paper trail. Draw the whole track of point R until the s
It is given segment AB, which is 12 cm in length, on which one side of the square MRAK is laid. MRAK's side length is 2 cm shown. MRAK gradually flips along the line segment AB, and point R leaves a paper trail. Draw the whole track of point R until the s - Hypotenuse - RT
 A triangle has a hypotenuse of 55 and an altitude to the hypotenuse of 33. What is the area of the triangle?
A triangle has a hypotenuse of 55 and an altitude to the hypotenuse of 33. What is the area of the triangle? - Simultaneously 6997
 Two boys train to run on a 400 m closed track. They both run simultaneously from the same starting track in the same direction. Boy A runs at a constant speed of 5 m/s, and Boy B runs at a constant speed of 3 m/s. At what time does Boy A overtake Boy B fo
Two boys train to run on a 400 m closed track. They both run simultaneously from the same starting track in the same direction. Boy A runs at a constant speed of 5 m/s, and Boy B runs at a constant speed of 3 m/s. At what time does Boy A overtake Boy B fo - Circle - analytics geometry
 Write the equation of the circle that passes through the points Q[3.5] R[2.6] and has its center on the line 2x+3y-4=0.
Write the equation of the circle that passes through the points Q[3.5] R[2.6] and has its center on the line 2x+3y-4=0. - Sum of inner angles
 Prove that the sum of all inner angles of any convex n-angle equals (n-2).180 degrees.
Prove that the sum of all inner angles of any convex n-angle equals (n-2).180 degrees. - Proof I
 When added to the product of two consecutive integers larger one, we get the square larger one. Is this true or not?
When added to the product of two consecutive integers larger one, we get the square larger one. Is this true or not? - Coordinate 82855
 What is the ratio of the distance of the nearest and farthest point of the circle described by the equation x2+y2-16x-12y+75=0 from the origin of the coordinate system?
What is the ratio of the distance of the nearest and farthest point of the circle described by the equation x2+y2-16x-12y+75=0 from the origin of the coordinate system? - Rhombus construct
 Construct parallelogram (rhombus) ABCD, | AB | = 4 cm alpha = 30° and | BD | = 5 cm.
Construct parallelogram (rhombus) ABCD, | AB | = 4 cm alpha = 30° and | BD | = 5 cm. - Backpack carrying
 Aleš, Karel, and Simon went on a trip at 6:45. They arrived at the finish line at 9:15. They carried one backpack with them and took turns after 20 minutes. Karel carried the first section, and at 8.30 by Simon. a) Who carried the backpack in the second s
Aleš, Karel, and Simon went on a trip at 6:45. They arrived at the finish line at 9:15. They carried one backpack with them and took turns after 20 minutes. Karel carried the first section, and at 8.30 by Simon. a) Who carried the backpack in the second s - Similarity
 Are two right triangles similar if the first one has an acute angle 60° and the second one has an acute angle 30°?
Are two right triangles similar if the first one has an acute angle 60° and the second one has an acute angle 30°? - Boat in the lake
 A boatman walks along the ship's deck at a constant speed of 5 km/h in a direction that forms an angle of 60° with the direction of the ship's speed. The boat moves with respect to the lake's calm surface at a constant speed of 10 km/h. Determine graphica
A boatman walks along the ship's deck at a constant speed of 5 km/h in a direction that forms an angle of 60° with the direction of the ship's speed. The boat moves with respect to the lake's calm surface at a constant speed of 10 km/h. Determine graphica - Distances
 A boy is rowing a boat at a speed of 7.2 km/h. He directed the boat perpendicularly to the opposite bank, which is 600 m away. The river carries the boat at a speed of 4.0 km/h. What is the resulting speed of the boat relative to the bank? How far will th
A boy is rowing a boat at a speed of 7.2 km/h. He directed the boat perpendicularly to the opposite bank, which is 600 m away. The river carries the boat at a speed of 4.0 km/h. What is the resulting speed of the boat relative to the bank? How far will th - Two-dimensional 36453
 Two of its inhabitants stand at one point in the land of two-dimensional beings. Suddenly, they both start running at the same moment. Resident A runs north at 5m/s, and resident B runs east at 12m/s. Calculate how fast they are moving away from each othe
Two of its inhabitants stand at one point in the land of two-dimensional beings. Suddenly, they both start running at the same moment. Resident A runs north at 5m/s, and resident B runs east at 12m/s. Calculate how fast they are moving away from each othe
Do you have homework that you need help solving? Ask a question, and we will try to solve it. Solving math problems.
