Planimetrics - math word problems - page 168 of 185
Number of problems found: 3685
- Degrees 70334
 What is the height of a diamond with a side 6 cm long if the angle formed by the sides is 78 degrees and 10 '?
What is the height of a diamond with a side 6 cm long if the angle formed by the sides is 78 degrees and 10 '? - Calculate 3209
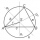 Calculate the lengths of the sides of the triangle ABC, in which angles α = 113°, β = 48°, and the radius of the circle of the triangle described is r = 10 cm.
Calculate the lengths of the sides of the triangle ABC, in which angles α = 113°, β = 48°, and the radius of the circle of the triangle described is r = 10 cm. - Calculate 43331
 From the lookout tower, 70 meters high, we see a man at a depth angle of 15 degrees. Calculate how far one stands from the base of the lookout tower. Draw and calculate.
From the lookout tower, 70 meters high, we see a man at a depth angle of 15 degrees. Calculate how far one stands from the base of the lookout tower. Draw and calculate. - Difference 4749
 How big a difference in altitude will the cable car overcome when it rises 1200 m at a 70-degree angle?
How big a difference in altitude will the cable car overcome when it rises 1200 m at a 70-degree angle? - Building elevation angle
 In the building, I focused at an angle 30°. When I moved the 5 m building, I focused at an angle 45°. What is the height of the building?
In the building, I focused at an angle 30°. When I moved the 5 m building, I focused at an angle 45°. What is the height of the building? - Triangle TBC
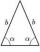 TBC is an isosceles triangle with base TB with base angle 75° and legs length |TC| = |BC| = 35. How long is the base TB?
TBC is an isosceles triangle with base TB with base angle 75° and legs length |TC| = |BC| = 35. How long is the base TB? - Parallelogram - area
 Calculate the area of the parallelogram if the sides are a = 80, b = 60 long, and the size of the diagonal angle is 60°.
Calculate the area of the parallelogram if the sides are a = 80, b = 60 long, and the size of the diagonal angle is 60°. - Sun and shadow
 The pole is stuck vertically into the ground. The protruding length is 1m. What is the length of the shadow cast when the sun is just 50° above the horizon?
The pole is stuck vertically into the ground. The protruding length is 1m. What is the length of the shadow cast when the sun is just 50° above the horizon? - An angle of depression
 The lighthouse sees a ship at an angle of depression of 25°. The observer from the lighthouse is 82 m above sea level. How far is the ship from the top of the lighthouse?
The lighthouse sees a ship at an angle of depression of 25°. The observer from the lighthouse is 82 m above sea level. How far is the ship from the top of the lighthouse? - The mast
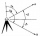 We see the top of the pole at an angle of 45°. If we approach the pole by 10 m, we see the top of the pole at an angle of 60°. What is the height of the pole?
We see the top of the pole at an angle of 45°. If we approach the pole by 10 m, we see the top of the pole at an angle of 60°. What is the height of the pole? - Right triangle
 Calculate the length of the remaining two sides and the angles in the rectangular triangle ABC if a = 10 cm, angle alpha = 18°40'.
Calculate the length of the remaining two sides and the angles in the rectangular triangle ABC if a = 10 cm, angle alpha = 18°40'. - Parallelogram
 We know about parallelogram ABCD: length |AB| = 76cm, |BC| = 44cm, and angle ∢BAD = 30°. Find the area of the parallelogram.
We know about parallelogram ABCD: length |AB| = 76cm, |BC| = 44cm, and angle ∢BAD = 30°. Find the area of the parallelogram. - Hexagon 5
 The distance of parallel sides of regular hexagons is 97 cm. Calculate the length of the radius of the circle described in this hexagon.
The distance of parallel sides of regular hexagons is 97 cm. Calculate the length of the radius of the circle described in this hexagon. - Cosine
 The point (3, 4) is on the terminal side of angle θ. cos θ = ...
The point (3, 4) is on the terminal side of angle θ. cos θ = ... - Triangle
 Calculate the area of the triangle ABC if b = c = 17 cm, R = 19 cm (R is the circumradius).
Calculate the area of the triangle ABC if b = c = 17 cm, R = 19 cm (R is the circumradius). - Regular 5-gon
 Calculate the area of the regular pentagon with side 16 cm.
Calculate the area of the regular pentagon with side 16 cm. - Cable car
 The cable car rises at an angle of 44° and connects the upper and lower station with an altitude difference of 1089 m. How long is an "endless" tow rope?
The cable car rises at an angle of 44° and connects the upper and lower station with an altitude difference of 1089 m. How long is an "endless" tow rope? - Kites
 Boys run kites on a cable of 68 meters long. What is the kite altitude if the angle from the horizontal plane is 72°?
Boys run kites on a cable of 68 meters long. What is the kite altitude if the angle from the horizontal plane is 72°? - Jewel
 Rhombus-shaped jewel has an area of 109 mm², and the edge is long 13 mm. Calculate the size of the acute rhombus angle.
Rhombus-shaped jewel has an area of 109 mm², and the edge is long 13 mm. Calculate the size of the acute rhombus angle. - Triangle SAA
 The triangle has one side long 23 m, and its two internal angles are 60°. Calculate the perimeter and area of the triangle.
The triangle has one side long 23 m, and its two internal angles are 60°. Calculate the perimeter and area of the triangle.
Do you have homework that you need help solving? Ask a question, and we will try to solve it. Solving math problems.
