Pythagorean theorem - math word problems - page 61 of 73
Number of problems found: 1446
- The gable
The house's gable is an isosceles triangle with a base length of 14 meters and arms lengths of 8 meters. What is the tall gable of the house? - Isosceles + prism
Calculate the volume of the perpendicular prism if its height is 17.5 cm and the base is an isosceles triangle with a base length of 5.8 cm and an arm's length of 3.7 cm. - Rotating cone
If the side of the rotating cone is 150 mm long and the circumference of the base is 43.96 cm, find its surface and volume. - Sphere parts, segment
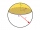A sphere with a diameter of 20.6 cm, the cut is a circle with a diameter of 16.2 cm. What are the volume and surface of the segment? - Regular quadrilateral pyramid
What is the volume of a regular quadrilateral pyramid if its surface is 576 cm² and the base edge is 16 cm? - Truncated cone 6
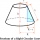Calculate the volume of the truncated cone whose bases consist of an inscribed circle and a circle circumscribed to the opposite sides of the cube with the edge length a=1. - Cone roof
How many m² of roofing is needed to cover a cone-shaped roof with a diameter of 10 m and a height of 4 m? Add an extra 4% to the overlays. - Hexagonal pyramid
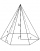Please calculate the height of a regular hexagonal pyramid with a base edge of 5cm and a wall height of w = 20cm. Please sketch a picture. - Pyramid height
Find the volume of a regular triangular pyramid with edge length a = 12cm and pyramid height h = 20cm. - Pyramid in cube
In a cube with an edge 12 dm long, we have an inscribed pyramid with the apex at the center of the cube's upper wall. Calculate the volume and surface area of the pyramid. - The roof of the church
The cone roof of the church has a diameter of 3 m and a height of 4 m. What is the size of the side edge of the church roof (s=?), and how many sheets of the sheet will be needed to cover the church roof? - Triangular prism
The base of the perpendicular triangular prism is a right triangle with a leg length of 5 cm. The area of the largest sidewall of its surface is 130 cm², and the body's height is 10 cm. Calculate its volume. - Stadium
A domed stadium is shaped like a spherical segment with a base radius of 150 m. The dome must contain a volume of 3500000 m³. Determine the dome's height at its center to the nearest tenth of a meter. - Sphere - parts
Calculate the area of a spherical cap, which is part of an area with a base radius ρ = 8 cm and a height v = 4.2 cm. - Spherical cap
From the sphere with a radius of 26 was a truncated spherical cap. Its height is 2. What part of the volume is a spherical cap from the whole sphere? - Quadrilateral 83254
What is the volume of a regular quadrilateral pyramid if its base edge a = √18 cm and side edge b = 5 cm? - Precisely 82088
A regular helix is drawn on the shell of the cylinder such that it wraps around the cylinder precisely three times (that is, the point where it touches the upper base is exactly above the point where it touches the lower base). If the diameter of the cyli - The regular
The regular triangular prism has a base in the shape of an isosceles triangle with a base of 86 mm and 6.4 cm arms; the height of the prism is 24 cm. Calculate its volume. - Diagonal 8192
Find the volume and surface of a cube if you know the length of its body diagonal u = 216 cm. - Quadrilateral 8120
If the pyramid's height is 4 cm and the base area is 16 cm2, include the side edge length of a regular quadrilateral pyramid.
Do you have unsolved math question and you need help? Ask a question, and we will try to solve it. We solve math question.
