Normálne rozdelenie - príklady
Používa sa pri náhodných veličinách, ktoré sú súčtom veľkého počtu nezávislých alebo len slabo závislých hodnôt. Rozloženie pravdepodobností má zvonovitý tvar - Gaussova krivka. Je symetrické okolo strednej hodnoty μ, ktorá je súčasne mediánom aj modusom. Pravidlo troch sigma (sigma σ=smerodajná odchýlka): od strednej hodnoty μ do vzdialenosti σ patrí 68,26% pravdepodobnosti, do 2σ leží 95,45%, do 3σ 99,73%.Počet nájdených príkladov: 26
- Poisťovňa
Poisťovňa dostane v priemere dve škody týždenne z konkrétnej továrne za predpokladu, že počet škôd možno modelovať podľa Poissonovho rozdelenia, nájdite pravdepodobnosť, že dostane tri nároky v danom týždni, viac ako štyri nároky v danom týždni, štyri nár - Pravdepodobnosť 74714
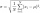Váhy rýb v určitom jazere je normálne rozdelená s priemerom 11 lb (libier) a štandardnou odchýlkou 6 lb. Ak sú náhodne vybrané 4 ryby, aká je pravdepodobnosť, že priemerná hmotnosť bude medzi 8,6 a 14,6 lb? Vašu odpoveď zaokrúhlite na štvrté desatinné m - Pravdepodobnosť 73204
Predpokladajme, že životnosť revolučnej žiarovky je normálne rozložená so strednou životnosťou 70 tisíc hodín a smerodajnou odchýlkou 3 tisíc hodín. Ak sa žiarovka vyberie náhodne: a) aká je pravdepodobnosť, že dĺžka života bude do 5 000 hodín od prieme - Odvážnejších 73154
Joanin cieľový čas v odvážnejších pretekoch na 10 km bol o 1,77 štandardnej odchýlky rýchlejší ako ženy v jej vekovej skupine. V jej vekovej kategórii kandidovalo 415 žien. Za predpokladu normálneho rozloženia, koľko žien bežalo rýchlejšie ako Joan? - Pravdepodobnosť 72834
Pravdepodobnosť, že životnosť žiarovky bude viac ako 682 hodín, je 0,9788. Pravdepodobnosť, že žiarovka bude mať životnosť viac ako 703 hodín, je 0,0051. Nájdite pravdepodobnosť, že žiarovka vydrží viac ako 648 hodín. - Pravdepodobnostiach 71824 Majme automatickú linku na výrobu kuchynských robotov. Chceme pomôcť Waldovmu testu otestovať, či podiel chybných robotov nepresahuje 5% o viac ako 1%. Testovať môžeme až 200 robotov naraz. Náklady na vykonaný test sú 50 Kc na spotrebu el. energie na každ
- Prepitné
V gastronomickom zariadení sa vždy na konci dňa robí inventúra v pokladnici, aby si mohli zamestnanci rozdeliť prepitné. Zistilo sa, že denné prepitné sa riadi normálnym rozdelením so strednou hodnotou 130 € a smerodajnou odchýlkou 60. Aká je pravdepodobn - Dve sigma Čas potrebný na vypracovanie testu má normálne rozdelenie so strednou hodnotou 50 minút a smerodajnou odchýlkou 10 minút. Koľko percent študentov vypracuje test do 30 minút?
- Pravdepodobnosti 65614
Hmotnosti žalúdka sú normálne rozdelené, s priemerom 1314 g a štandardnou odchýlkou 113 g. Uveďte pravdepodobnosť, že náhodne vybraný žalúdok váži viac ako 1118 g. (Vypočítajte pravdepodobnosti s použitím aspoň 4 desatinných miest. ) - Pravdepodobnosť 54561
Predpokladajme, že 14 % všetkých oceľových hriadeľov vyrobených určitým procesom je nezhodných, ale možno ich prepracovať (a nie zošrotovať). Zoberme si náhodnú vzorku 200 hriadeľov a nech X označuje počet z nich, ktoré nie sú v súlade a môžu byť prepraco - Štandardizovaný
Štandardizovaný test bol podaný tisícom študentov s priemerným skóre 85 a štandardnou odchýlkou 8. Náhodná vzorka 50 študentov dostala rovnaký test a vykázala priemerné skóre 83,20. Existujú dôkazy, ktoré preukazujú, že táto skupina má na úrovni 0,05 nižš - Respondenti - chí kvadrát Opýtaní respondenti odpovedali na otázku o ich priemernej čistej mesačnej mzde. Uvedené odpovede sú v tis. €: 0,40; 0,60; 0,55; 0,68; 0,63; 0,70; 0,65; 0,75; 0,91; 0,63; 0,38; 0,39; 0,38; 0,74; 1,25; 1,10; 1,30; 1,15; 1,18; 1,13; 1,15; 1,19; 1,21. Pomocou
- Chí kvadrát 2 Nech za posledných 14 rokov mala krajina tieto miery inflácie: 6,0; 6,7; 10,4; 11,9; 7,2;3,5; 8,4; 7,5; 2,8; 4,3; 1,9; 3,9; 0,9; 0,7. Pomocou χ² testu dobrej zhody zistite, či náhodná veličina ξ odpovedajúca tejto miere inflácie má normálne rozdelenie ale
- Chi kvadrát Porovnával sa počet zamestnancov v oblasti kultúry v krajine A a v krajine B. Zistili sa tieto počty zamestnancov v tis. Osôb: krajina A x/46/45/41/48/49/ krajina B y/128/135/147/152/148/. Na hladine testu α=0,05 zistite, či počet zamestnancov v oblasti k
- Bernoulli
Polícia v sledovanom období riešila 21 trestných činov. Pravdepodobnosť vyriešenia trestného činu je 0,64. Aká je pravdepodobnosť, že polícia: a) vyriešila práve 7 trestných činov b) nevyriešila aspoň 2 trestné činy PS. Predpokladajme ideálnych policajtov - Horolezec
Horolezec plánuje kúpiť nejaké lano, ktoré použije ako záchranné lano. Ktorá z nasledujúcich možností by bola lepšou voľbou? Vysvetlite svoj výber. Lano A: Stredná pevnosť v ťahu: 500 libier; štandardná odchýlka 100 libier Lano B: Stredná pevnosť v ťahu: - Holanďania 36141 Holanďania ako skupina patria medzi najvyšších ľudí na svete. Priemerný Holanďan je vysoký 184 cm. Ak je vhodné normálne rozdelenie a štandardná odchýlka pre Holanďanov je asi 8 cm, aké je percento Holanďanov, ktorí budú mať viac ako 2 metre?
- IQ Inteligenčný kvocient, Inteligenčný kvocient, (IQ), je štandardizované skóre používané ako výstup štandardizovaných inteligenčných psychologických testov k vyčíslenie inteligencie človeka v pomere k ostatnej populácii (respektíve k danej skupine). Inteligencia má približne norm
- Pri hromadnej
Pri hromadnej výrobe výrobku je priemerný rozmer 250mm, pričom rozmery jednotlivých výrobkov vplyvom nepresností pri výrobe kolíšu okolo tejto strednej hodnoty. Rozmer výrobkov má normálne rozdelenie so smerodajnou odchýlkou a=10mm a) Aká je pravdepodnosť - Životnosť 2
Životnosť žiarovky je náhodnou premennou s normálnym rozdelením x=300 hodín, σ=35 hodín. a) Aká je pravdepodobnosť toho, že náhodne vybraná žiarovka bude mať životnosť väčšiu ako 320 hodín? b) Do akej hodnoty L hodín možno s pravdepodobnosťou 0,25 očakáva
Máš úlohu, nad ktorou si lámeš aspoň 10 minút hlavu? Pošli nám úlohu a my Ti ju skúsime vypočítať.
