Prvočísla - slovné úlohy a príklady - strana 16 z 27
Počet nájdených príkladov: 524
- Pagáče
Elena vykrojila z cesta 15 rovnakých pagáčov v tvare kruhu a uložila ich na obdĺžnikový plech tak, aby sa susedné pagáče navzájom dotýkali a pagáče sa po okrajoch dotýkali stien plechu. Každý pagáč zaberal 28,26 cm² dna plechu. Aké rozmery má dno plechu? - Násobok - NSN
Najmenší násobok čísla 63 a 147 - NSM 2
Najmenší spoločný menovateľ zlomkov 2/5, 1/2 a 3/4 - Predaje
Za 80 výrobkov dvojakej akosti sa utŕžilo celkom 175 Eur. Ak výrobok prvej kvality sa predával po n Eur za kus (n prirodzené číslo) a výrobok druhej akosti po dvoch Eur za kus, koľko kusov prvej kvality bolo predaných? - Izby v ubytovni
V ubytovni je 32 izieb. Niektoré sú dvojlôžkové, iné štvorlôžkové a zvyšné majú 7 lôžok. Celkom je v celej ubytovni 139 lôžok. Koľko je ktorých, ak počty jednotlivých druhov sú dané dvojciferným číslom? - Čokoláda 6
Medzinárodná banda pašerákov čokolády vedená slávnym Jackom Krivým Nosom, ktorý má 7 spolupracovníkov, si vytipovalal bratislavské letisko ako križovatku svojich obchodov. Lietadlo z Bratislavy do Štokholmu lieta každý tretí deň. Lietadlo z Bratislavy do - Bicykle
Si majiteľ dopravného ihriska. Kúp bicykle dvoch farieb ľubovoľného počtu, ale musíš minúť presne 120000 Kč. Modrý bicykel stojí 3600 Kč a červený bicykel stojí 3200 Kč. - Paša
Obdĺžnikovú lúku s rozmermi 1280 m a 320 m rozdeľte na štvorcové pastviská s čo najdlhšou stranou štvorca. Na koľko štvorcových pastvísk ste rozdelili lúku? - Čísla 9 Koľko trojcifernych čísel delitelnych číslom štyri môžeme vytvoriť z čísel 1;2;3; a 5, ak sa číslice v čísle nemôžu opakovať?
- Ciferny súčet 27 Ktoré najväčšie šesťciferné číslo má ciferný súčet 27?
- Narodeninové voľno
Moje číslo na dnes: súčin druhej mocniny najmenšieho prvočísla s najmenším dvojciferným prvočíslom - Kocky
Karol s Milanom rozrezali trámik 12 cm krát 12 cm krát 135 cm na kocôčky. Vypočítaj hodnotu udávajúce súhrn povrchov všetkých takto vzniknutých kociek. - Krabica
Navrhnite veľkosť najmenšej možnej krabica v tvare kocky do ktorej by bolo možné naskladať tri druhy hracích kociek s dĺžkou hrany 3 cm, 5 cm, 6 cm tak, aby bol priestor krabice úplne využitý (každý typ kocky samostatne). Dokážete zistiť, koľko najmenších - MO Z6-6-1
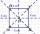
Do prázdnych polí v nasledujúcom obrázku doplňte celé čísla väčšie ako 1 tak, aby v každom tmavšom políčku bol súčin čísel zo susedných svetlejších políčok: Aké je číslo je v strede? - Autíčka Pavel má zbierku autíčok. Chcel je novo usporiadať do skupín. Ale pri delení po troch, po štyroch, po šiestich i po ôsmich mu vždy jedno zostalo. Až keď tvoril skupiny po siedmich, rozdelil všetky. Koľko má autíčok v zbierke?
- Čísla a, nájdi najväčšie prirodzené číslo , ktorým sa dajú vydeliť čísla 54 aj 72 ( 120 , 60 aj 42 ) b, nájdi najmenšie prirodzené číslo, ktoré sa dá vydeliť každým z čísel 36 a 48 ( 24,18 a 16 )
- Delenie laty
1. lata 2,5 m, 2. lata 1,75 m. Koľko dielikov čo najväčších? Rozmer 1 dielika? - Veľká Pardubická
Jirka sa rozhodol, že výhru zo stávky vo Veľkej pardubickej rozdelí medzi seba a troch svojich mladších bratov podľa veku v pomere 2:3:5:7. Každá čiastka bola vyplatená v celých korunách. Jedna z čiastok bola 679kč. Aká veľká bola výhra? - Rozdelenie
Riaditeľ školy uvažoval či rozdelenie žiakov pri orientačnom závode do skupín po 4,5,6,9 alebo 10. Koľko musí mať najmenej škola žiakov ak sú možné všetky varianty? - Stretnutie sprievodcov
Návštevníci zámku si môžu vybrať z troch prehliadkových okruhov, ktoré trvajú aj s krátkou prestávkou pre sprievodcov 35, 50 a 70 minút. O 8 hodine vyjdú sprievodcovia so svojimi skupinami na trasu. Za ako dlho by sa opäť všetci stretli, keby každý sprevá
Máš úlohu, ktorú si tu nenašiel vyriešenú? Pošli nám túto úlohu a my Ti ju skúsime vypočítať. Riešime príklady a úlohy z matematiky. Nielen domáce.
