Príklady pre stredoškolákov - strana 140 z 225

Počet nájdených príkladov: 4484

Kváder
Kváder má objem 32 cm³ . Jeho plášť má dvojnásobný obsah ako jedna zo štvorcových podstáv. Akú dĺžku má telesová uhlopriečka?
Strany trojuholníka
Ak jednu stranu trojuholníka zväčšíme o 11 cm a druhú zmenšíme o 11 cm, dostaneme rovnostranný trojuholník. Štvornásobok najkratšej strany trojuholníka je o 10 cm väčší ako trojnásobok najdlhšej strany trojuholníka. Zisti všetky dĺžka strán trojuholníka
Nárast obyvateľstva
Počet obyvateľov je 22000 osôb. Pri ročnom náraste 1,4% ich bude 25000 osôb. Za koľko rokov to tak bude?
Trať pretekov
Cyklistické preteky mali 4 etapy. Dĺžka prvej bola 1/3 dĺžky celej trate. Dĺžka druhej etapy bola 2/9 dĺžky celej trate a dĺžka tretej etapy 1/4 trate. Štvrtá eapa bola o 15 km kratšia ako druhá etapa. Aká dlhá bola trať celých pretekov?
Lekáreň
V lekárni priliali k 3 litrom 95- percentného liehu 5 litrov 38,04-percentného liehu. Koľko percentný lieh dostal?
Letiská
Medzi dvoma letiskami je vzdialenosť 3480 km, lietaju pravidelne spoje z letiska 1 startuje lietadlo o 6:30 priemernou rýchlosťou 600km/h. Z letiska 2 o 7:00 lietadlo rýchlosťou 540km/h. Kedy sa stretnú?
Rady práškov
200 krabíc pracích práškov bolo v obchode narovnaných v 3 radoch. V prvom rade bolo o 13 krabíc viac ako v druhom, v druhom o jednu pätinu viac ako v treťom rade. Koľko krabíc bolo v jednotlivých radoch?
Odvesny a prepona
Prepona pravouhlého trojuholníka je o 9 cm dlhšia než jedna odvesna a o 8 cm dlhšia než druhá odvesna. Určte obvod a obsah trojuholníka.
Tretiny
Prvú tretinu dráhy prešiel automobil rýchlosťou 15km/h, druhú tretinu rýchlosťou 30 km/h a poslednú tretinu rýchlosťou 90 km/h. Určte priemernú rýchlosť pohybu auta.
MO - bikvadrát
Nájdite najväčšie prirodzené číslo d, ktoré má tú vlastnosť, že pre ľubovoľné prirodzené číslo n je hodnota výrazu V(n)=n⁴+11n²−12 deliteľná číslom d.
Otáčanie štvorca
Štvorec o strane dĺžky 3 cm sa otáča okolo svojej uhlopriečky. Vypočítajte objem a povrch vzniknutého telesa
Trojčlen P(x)
Nájdete všetky trojčleny P(x) = a * x² + b * x + c s celočíselnými koeficientmi a, b a c, pre ktoré platí P(1) < P(2) < P(3) a zároveň ((P(1)) ² + ((P(2)) ² + ((P(3)) ² = 22).
Dôkaz - MO - C – I – 3
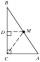Päta výšky z vrcholu C v trojuholníku ABC delí stranu AB v pomere 1:2. Dokážte, že pri zvyčajnom označení dĺžok strán trojuholníka ABC platí nerovnosť 3|a-b| < c.
Ťažisko
V trojuholníku ABC s ťažiskom T platí b=7cm, tc=9cm uhol ATC je 112 stupňov. Vypočítajte dĺžku ťažnice ta.
Ťažnice
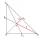Vypočítajte obsah trojuholníka ABC ak platí a= 10 cm, c=8 cm, ta=6 cm.
Omega
Vypočítaj obvod trojuholníka ABC ak platí a=12 cm, uhol beta je 38stupnov a gama je 92 stupňov.
Roztoky 8
Do roztoku, ktorý obsahoval 400 g soli, bolo pridané 300 g vody. Tým sa koncentrácia roztoku znížila o 5%. Koľko vody obsahoval pôvodný roztok a akú mal koncentráciu?
Matička
Určte, koľko riadkov obsahuje štvorcová matica 7.rádu.
Matica 3x3
Určte, koľko prvkov obsahuje štvorcová matica tretieho rádu.
Krčmička
V jednej nemenovej pražskej krčmičke merala ČOI točené veľké pivá. Z tridsiatich nameraných pollitrov vyšiel výberový priemer 0,457085 l a výberová smerodajná odchýlka 0,00303. Otestujte na hladine 1% a 5% hypotézu, že výčapný točí správnu mieru (tj. prot

Máš úlohu, ktorú si tu nenašiel vyriešenú? Pošli nám túto úlohu a my Ti ju skúsime vypočítať. Riešime príklady a úlohy z matematiky. Nielen domáce.