Príklady pre stredoškolákov - strana 18 z 224
Počet nájdených príkladov: 4465
- Kombinácií 80637
Ak sa zmenší počet prvkov o 4, zmenší sa počet kombinácií druhej triedy z týchto prvkov trikrát. Koľko je prvkov? - Auto zastavilo
Auto zastavilo pri začiatočnej rýchlosti 90 km/hod na dráhe 62,5 m. Aké bolo jeho zrýchlenie a aký čas trvalo brzdenie auta? - Románopisec JV
Francúzsky románopisec Jules Verne napísal román, v ktorom bola vyslovená myšlienka vyslať na mesiac veľkú delovú strelu s ľudskou posádkou vo vnútri. Telová hlaveň, z ktorých bola strela vystrelená, mala dĺžku 220m. a) Ako dlho by si si strela pohybovala - Učiteľov 80619
Vek 10 učiteľov školy je 32, 41, 67, 55, 23, 25, 28, 40, 22, 35 rokov. Zistite vekový rozsah učiteľov. - Kružnici
Kružnici je opísaný a vpísaný pravidelný šesťuholník. Rozdiel ich obsahov je 8√3. Určte polomer kružnice. - Striedavý prúd
V striedavom obvode je celkové napätie V dané vzťahom V=V1 + V2 Ak V=(12,2+6,8i) V a V1=(7,8-2,5i) V, nájdite napätie V2. - Pochod podľa kompasu
Muž v púšti prejde 8,7 míle v smere S 26° W (juho-západ). Potom sa otočí o 90° a prejde 9 míľ v smere na N 49° W (severo západne). Ako ďaleko je v tom čase od svojho východiskového bodu a jeho postoj od jeho východiskového bodu? - Charakteristiky 80608 Bol vypočítaný aritmetický priemer xA=40 a štandardná odchýlka sx=8. Určite z ktorých čísel boli uvedené charakteristiky vypočítané: a) 24 a 56 b) 16 a 64 c) 32 a 48
- Žiarovku
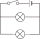Žiarovku 2,5 V, 0,3 A chceme pripojiť na plochú batériu. Aký veľký odpor a akým spôsobom musíme k žiarovke pripojiť? - Pomer 9
Pomer súčasného veku Raula a Rohita je 5:7. Pred štyrmi rokmi bol vek Rohita o 12 vyšší ako vek Raula. Potom nájdite ich súčasný vek. - L Hopitalovo pravidlo
Na riešenie použite L Hopitalovo pravidlo (i) Lim x²+5x-14/x²-5x+6 X—>2 (ii) Lim x³+x²-x-1/x²-2x-3 X—>3 - Vo vetve
Vo vetve s odporom 5 ohmu tiekol prúd 0,1 A. V druhej vetve prúd 0,2 A. Vypočítajte: a) aký je odpor druhej vetvy, b) na aké napätie bol obvod pripojený. - Dva rezistory Dva rezistory 6 ohmov a 8 ohmov sú zapojené paralelne k plochej batérii U=4,5 V. Vypočítajte: a) celkový prúd, b) prúd vo vetvách.
- Dva vodiče Dva vodiče majú pri sériovom spojení odpor Rs=5 ohmov a pri paralelnom Rp=1,2 ohmov. Vypočítajte veľkosť odporov.
- Projektil 2
Projektil o hmotnosti 20 g vystrelí rýchlosťou 800 m/s sa zaryje 100 mm hlboko do zdiva. Ako dlho vo zdive brzdí za predpokladu rovnomerne zpomaleného pohybu. - Pravdepodobnosť troch porúch
Mám 3 zdroje a ich pravdepodobnosť poruchy je 0,1. Vypočítaj, aká bude pravdepodobnosť, že: a) žiadny nebude mať poruchu b) 1 bude mať poruchu c) alepoň 1 bude mať poruchu d) všetky budú mať poruchu - Vzdialenosť 80542
Nájdite na číselnej osi číslo, ktorého vzdialenosť od čísla 3 je štyrikrát menšia ako od čísla 15 (určte obe riešenia). - Podmienená pravdepodobnosť
Výrobok má s pravdepodobnosťou 10 % vzhľadovú chybu, s pravdepodobnosťou 6 % funkčnú chybu a s pravdepodobnosťou 3 % obidve chyby súčasne. Sú náhodné udalosti A - výrobok má vzhľadovú chybu a B - výrobok má funkčnú chybu, nezávislé? - Aký odpor Aký odpor má dvojvodičové vedenie dlhé 10 m zhotovené z hliníkového drôtu s prierezom 4,0 mm²?
- Potenciálnu 80527
Kameň s hmotnosťou 2 kg padá voľným pádom z veže s výškou 80 m. Akú má kinetickú energiu a akú potenciálnu energiu: a) Na začiatku pádu, b) V čase 1 s od začiatku pádu, c) Pri dopade, d) Akú má počas pádu mechanickú energiu vzhľadom na povrch Zeme?
Máš príklad, ktorý si tu nenašiel vyriešenú? Pošli nám príklad a my Ti ho skúsime vypočítať.
