Príklady pre stredoškolákov - strana 88 z 225
Počet nájdených príkladov: 4484
- Z8 – I – 1 MO 2019
 Zostrojte kosoštvorec ABCD tak, aby jeho uhlopriečka BD mala veľkosť 8 cm a vzdialenosť vrcholu B od priamky AD bola 5 cm. Určte všetky možnosti. Aká je dĺžka strany kosoštvorca?
Zostrojte kosoštvorec ABCD tak, aby jeho uhlopriečka BD mala veľkosť 8 cm a vzdialenosť vrcholu B od priamky AD bola 5 cm. Určte všetky možnosti. Aká je dĺžka strany kosoštvorca? - Poklad
 Skauti majú stan v tvare pravidelného štvorbokého ihlanu so stranou podstavy 4 m a výške 3 m. Do stanu potrebujú schovať valcovú nádobu s tajným pokladom. Určte polomer r (a výšku h) nádoby tak, aby mohli schovať čo nejobjemnější poklad.
Skauti majú stan v tvare pravidelného štvorbokého ihlanu so stranou podstavy 4 m a výške 3 m. Do stanu potrebujú schovať valcovú nádobu s tajným pokladom. Určte polomer r (a výšku h) nádoby tak, aby mohli schovať čo nejobjemnější poklad. - Hmotný bod
 Hmotný bod sa pohybuje rovnomerne po kružnici s polomerom 1,2 m uhlovou rýchlosťou 25 rad/s. Určte frekvenciu, periódu a dostredivé zrýchlenie!
Hmotný bod sa pohybuje rovnomerne po kružnici s polomerom 1,2 m uhlovou rýchlosťou 25 rad/s. Určte frekvenciu, periódu a dostredivé zrýchlenie! - Kamaráti 5
 Erik sa kamaráti s dvoma dievčatami, Markétou a Lenkou a dvoma chlapcami, Tomášom a Robom. Keď jeho mama chcela vedieť, koľko majú tie deti rokov, povedal jej hádanku: Tomáš je o dva roky starší ako Robo. Súčet vekov chlapcov je rovnaký ako súčet vekov di
Erik sa kamaráti s dvoma dievčatami, Markétou a Lenkou a dvoma chlapcami, Tomášom a Robom. Keď jeho mama chcela vedieť, koľko majú tie deti rokov, povedal jej hádanku: Tomáš je o dva roky starší ako Robo. Súčet vekov chlapcov je rovnaký ako súčet vekov di - Sadrový odliatok
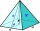 Sadrový odliatok má tvar pravidelného štvorbokého ihlanu. Plášť je tvorený štyrmi rovnostrannými trojuholníkmi so stranou 5 m. Vypočítajte jeho objem a povrch.
Sadrový odliatok má tvar pravidelného štvorbokého ihlanu. Plášť je tvorený štyrmi rovnostrannými trojuholníkmi so stranou 5 m. Vypočítajte jeho objem a povrch. - Rozkladací stôl
 Rozkladací kuchynský stôl má v bežnej podobe tvar obdĺžnika s obsahom 168dm² (strana a je dlhá 14 dm) . V prípade potreby sa môže zväčšiť vysunutím dvoch dosiek v tvare polkruhov (pri stranách b). O koľko percent sa takto zväčší plocha stola? Výsledok tre
Rozkladací kuchynský stôl má v bežnej podobe tvar obdĺžnika s obsahom 168dm² (strana a je dlhá 14 dm) . V prípade potreby sa môže zväčšiť vysunutím dvoch dosiek v tvare polkruhov (pri stranách b). O koľko percent sa takto zväčší plocha stola? Výsledok tre - Zemepis - test
 V troch 150-bodových zemepisných testoch ste získali známky 88 %, 94 % a 90 %. Záverečný test má hodnotu 250 bodov. Koľko percent potrebujete na finále, aby ste získali 93 % z celkového počtu bodov vo všetkých testoch?
V troch 150-bodových zemepisných testoch ste získali známky 88 %, 94 % a 90 %. Záverečný test má hodnotu 250 bodov. Koľko percent potrebujete na finále, aby ste získali 93 % z celkového počtu bodov vo všetkých testoch? - Výpočet z ťažníc
 Pravouhlý trojuholník, uhol C je 90 stupňov. Poznám ťažnicu ta = 8 cm a ťažnicu tb = 12 cm. .. Ako spočítať dĺžku strán?
Pravouhlý trojuholník, uhol C je 90 stupňov. Poznám ťažnicu ta = 8 cm a ťažnicu tb = 12 cm. .. Ako spočítať dĺžku strán? - Trojfázový účinník
 Dva wattmetre sú pripojené k meraniu výkonu pri 3 fázovom vyváženom zaťažení. Stanovte celkový výkon a účinník, ak dva wattmetre odčítajú 1 000 wattov (1) oba kladný a (2) druhý údaj záporný.
Dva wattmetre sú pripojené k meraniu výkonu pri 3 fázovom vyváženom zaťažení. Stanovte celkový výkon a účinník, ak dva wattmetre odčítajú 1 000 wattov (1) oba kladný a (2) druhý údaj záporný. - Domáce kino
 Domáce kino zlacnelo z pôvodnej ceny 710eur najskôr o 74 eur ešte o 32%. Za kolko eur bolo možné kupiť domáce kino po dvojnásobnom zlacnení
Domáce kino zlacnelo z pôvodnej ceny 710eur najskôr o 74 eur ešte o 32%. Za kolko eur bolo možné kupiť domáce kino po dvojnásobnom zlacnení - Stenové uhlopriečky
 Ak sú stenové uhlopriečky kvádra x, y a z (diagonály), potom nájdite objem kvádra. Vyriešte pre x=1,4, y=1,4, z=1,4
Ak sú stenové uhlopriečky kvádra x, y a z (diagonály), potom nájdite objem kvádra. Vyriešte pre x=1,4, y=1,4, z=1,4 - Voltmeter - rozsah
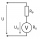 Máme voltmeter ktorý v originálnej zostave meria napätie do 10V. Vypočítajte veľkosť predradníka pre tento voltmeter, ak ním chceme merať napätie do 50V. Vnútorný odpor voltmetra je 2 kiloohm/Volt.
Máme voltmeter ktorý v originálnej zostave meria napätie do 10V. Vypočítajte veľkosť predradníka pre tento voltmeter, ak ním chceme merať napätie do 50V. Vnútorný odpor voltmetra je 2 kiloohm/Volt. - Odpis auta
 Sarah si kúpi auto za 12 500 dolárov. V prvom roku odpisuje hodnotu o 8 %, v druhom o 10 % a v treťom o 5 %. Vypočítajte hodnotu auta po treťom roku.
Sarah si kúpi auto za 12 500 dolárov. V prvom roku odpisuje hodnotu o 8 %, v druhom o 10 % a v treťom o 5 %. Vypočítajte hodnotu auta po treťom roku. - Stenové uhlopriečky
 Vypočítaj dĺžky stenových a telesových uhlopriečok kvádra s rozmermi hrán 0,5 m, 1 m a 2 m
Vypočítaj dĺžky stenových a telesových uhlopriečok kvádra s rozmermi hrán 0,5 m, 1 m a 2 m - Štvorboký ihlan
 Je daný pravidelný štvorboký ihlan. Dĺžka hrany podstavy a = 6,5 cm, bočná hrana s = 7,5 cm. Vypočítajte objem a obsah plášťa.
Je daný pravidelný štvorboký ihlan. Dĺžka hrany podstavy a = 6,5 cm, bočná hrana s = 7,5 cm. Vypočítajte objem a obsah plášťa. - Mimozemská loď
 Mimozemská loď má tvar gule o polomere r = 3000m a jej posádka potrebuje loďou odviezť nazbieraný výskumný materiál v boxe v tvare kvádra so štvorcovou podstavou. Určte dĺžku podstavy a (a výšku h) tak, aby mal box najväčší možný objem.
Mimozemská loď má tvar gule o polomere r = 3000m a jej posádka potrebuje loďou odviezť nazbieraný výskumný materiál v boxe v tvare kvádra so štvorcovou podstavou. Určte dĺžku podstavy a (a výšku h) tak, aby mal box najväčší možný objem. - Vrchol budovy
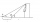 Z bodov A a B na rovnom povrchu sú uhly pozorovania vrcholu budovy 25° a 37°. Ak | AB | = 57 m, vypočítajte s presnosťou na najbližší meter vzdialenosti hornej časti budovy od A a B, ak sú obidve na tej istej strane budovy.
Z bodov A a B na rovnom povrchu sú uhly pozorovania vrcholu budovy 25° a 37°. Ak | AB | = 57 m, vypočítajte s presnosťou na najbližší meter vzdialenosti hornej časti budovy od A a B, ak sú obidve na tej istej strane budovy. - Zo 660
 Zo 660 žiakov školy je 60% dievčat. 25% dievčat chodí do 7 ročníka. Kolko dievčat školy chodí do 7 ročníka
Zo 660 žiakov školy je 60% dievčat. 25% dievčat chodí do 7 ročníka. Kolko dievčat školy chodí do 7 ročníka - Uhlopriečka kocky
 Priestorová uhlopriečka kocky je 129,91 mm. Nájdite bočnú plochu steny, povrch a objem kocky.
Priestorová uhlopriečka kocky je 129,91 mm. Nájdite bočnú plochu steny, povrch a objem kocky. - Trojdňový výlet
 Cyklista na trojdňovom výlete ušiel prvý deň 30% celkovej trasy, druhý deň 3/5 zvyšku a tretí deň 35 km. Koľko ušiel cyklista v jednotlivých dňoch a koľko celkom?
Cyklista na trojdňovom výlete ušiel prvý deň 30% celkovej trasy, druhý deň 3/5 zvyšku a tretí deň 35 km. Koľko ušiel cyklista v jednotlivých dňoch a koľko celkom?
Máš príklad, ktorý si tu nenašiel vyriešenú? Pošli nám príklad a my Ti ho skúsime vypočítať.
