Vrcholy 5
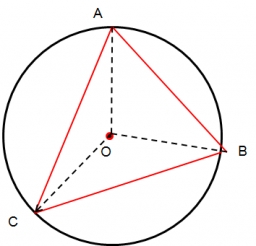
Vrcholy trojúhelníku ABC leží na kružnici k tak že ji dělí na tři díly v poměru 1:2:3. Sestroj tento trojúhelník.
Správná odpověď:
Tipy na související online kalkulačky
Vyzkoušejte naši kalkulačka na přepočet poměru.
Vyzkoušejte také naši trigonometrickou trojúhelníkovou kalkulačku.
Vyzkoušejte také naši trigonometrickou trojúhelníkovou kalkulačku.
K vyřešení této úlohy jsou potřebné tyto znalosti z matematiky:
geometrieplanimetriezákladní operace a pojmyJednotky fyzikálních veličintémaÚroveň náročnosti úkolu
Související a podobné příklady:
- Okruh
Vrcholy trojúhelníku ABC leží na kružnici s poloměrem 3 tak, že jí dělí na tři díly v poměru 4:4:4. Vypočítejte obvod trojúhelníku ABC. - Obvodový úhel
Vrcholy trojúhelníku ΔABC vepsaného do kružnice ji dělí na oblouky v poměru 7:8:9. Určete velikosti vnitřních úhlů ΔABC. - Trojúhelník konšt.
Narýsuj kružnici k(S, r=3cm). Sestroj trojúhelník ABC tak , aby jeho vrcholy ležely na kružnici k a délka stran byla (AB)=2,5cm (AC)=4cm - Vepsán trojúhelník
Do kružnice je vepsán trojúhelník tak, že jeho vrcholy dělí kružnici na 3 oblouky. Délky oblouků jsou v poměru 2:3:7. Urči vnitřní úhly trojúhelníka. - Čtyřúhelníku 82395
Body ABC leží na kružnici k(S, r) tak, že úhel u B je tupý. Jak velký musí být úhel u vrcholu B čtyřúhelníku SCBA, aby byl tento úhel třikrát větší než vnitřní úhel ASC téhož čtyřúhelníku? - Vepsány čtyřúhelník
Do kružnice je vepsán čtyřúhelník tak, že jeho vrcholy dělí kružnici 1:2:3:4. Vypočítejte velikosti jeho vnitřních úhlů. - Polopřímkách 80498
Daný je ostroúhlý trojúhelník ABC. Na polopřímkách opačných k BA a CA leží postupně body D a E tak, že |BD| = |AC| a |CE| = |AB|. Dokažte, že střed kružnice opsané trojúhelníku ADE leží na kružnici opsané trojúhelníku ABC.
