Zmetky
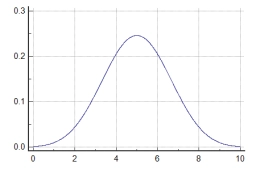
Při určité výrobě je pravděpodobnost výskytu zmetků 0,01. Vypočítejte, jaká bude pravděpodobnost, že mezi 100 vybranými výrobky bude více než 1 zmetek, pokud vybrané výrobky po kontrole vrátíme zpět do souboru.
Vaše odpověď:
Vaše odpověď:
Tipy na související online kalkulačky
K vyřešení této úlohy jsou potřebné tyto znalosti z matematiky:
statistikakombinatorikaÚroveň náročnosti úkolu
Související a podobné příklady:
- Pravděpodobnost - výrobky
Na základě předchozí kontroly je známo, že při výrobě určitého výrobku se vyskytují 3% zmetků. a) Vypočítejte pravděpodobnost jevu, že mezi 100 náhodně vybranými výrobky jsou právě 2 zmetky, přičemž každý výrobek po kontrole vrátíme do původního souboru. - Kontrola výrobků
V dávce 500 výrobků je 10 zmetků. Při statistické prověrce se kontroluje 40 výrobků, které jsou náhodně vybrány z dávky, přičemž se provádí výběr bez opakování. Dávka je posouzena jako vyhovující, pokud mezi 40 kontrolovanými výrobky je nejvýše jeden zmet - Kontrola zmetků
Ze série výrobků se má zkontrolovat 500 kusů, přičemž se provádí kontrola s opakováním. Výrobce garantuje při dané výrobě 2% zmetků. Určete pravděpodobnost, že mezi 500 kontrolovanými výrobky bude počet zmetků od 12 do 20. - Tombola
V osudí jsou čísla od 1 do 107. Jaká je pravděpodobnost, že náhodně vybrané číslo nebude prvočíslo? - Pravděpodobnost bílých kuliček
V krabici je 16 kuliček, z toho 7 bílých a 9 modrých. Náhodně vybereme 2 kuličky. Jaká bude pravděpodobnost, že mezi vybranými budou právě 2 bílé kuličky? - Pravděpodobnost prvotřídní kvality
Určitý výrobek můžeme vyrábět dvěma technologickými postupy. Pravděpodobnost prvotřídní kvality při prvním postupu je 0,68, při druhém 0,4. Všechny výrobky jsou uskladňovány společně. Prvním postupem vyrobíme 1,5x více výrobků než druhým. a) Jaká je pravd - Pravděpodobnost výběru hráče
Ze skupiny 18 hráčů, ve které jsem i já, vybere trenér 9 hráčů. Jaká je pravděpodobnost, že mezi vybranými hráči budu i já?
