MO Z6 I-3 2017 sklenice

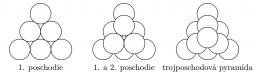
Honza měl 100 stejných zavařovacích sklenic, z kterých si stavěl trojboké pyramidy. Nejvyšší poschodí pyramidy má vždy jednu sklenici, druhé poschodí shora představuje rovnostranný trojúhelník, jehož strana sestává ze dvou sklenic, atd. Příklad konstrukce
trojposchoďové pyramidy je na obrázku.

1. Kolik sklenic Honza potřeboval na pětiposchoďovou pyramidu?
2. Kolik poschodí měla pyramida, na niž bylo použito co nejvíc Honzových sklenic?

Správná odpověď:

a =  35
b =  7

Postup správného řešení:

$$\begin{gathered} a_1=1 \\ {a}_2=2+1=3 \\ {a}_3=3+2+1=6 \\ {a}_4=4+3+2+1=10 \\ {a}_5=5+4+3+2+1=15 \\ a=a_1+a_2+a_3+a_4+a_5=1+3+6+10+15=35 \end{gathered}$$

$$\begin{gathered} a_6=6+a_5=6+15=21 \\ {s}_6=a+a_6=35+21=56 \\ {a}_7=7+a_6=7+21=28 \\ {s}_7=s_6+a_7=56+28=84 \\ {a}_8=8+a_7=8+28=36 \\ {s}_8=s_7+a_8=84+36=120 \\ {s}_7<100 \\ b=7 \end{gathered}$$

Zkusit jiný příklad