Dva úhly
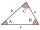
Trojúhelníky ABC a A'B'C 'jsou podobné. V trojúhelníku ABC jsou velikosti dvou úhlů 25° a 65°. Zdůvodnite, proč v trojúhelníku A'B'C 'je součet velikostí dvou c rovný 90°.
Správná odpověď:
Tipy na související online kalkulačky
Vyzkoušejte také naši trigonometrickou trojúhelníkovou kalkulačku.
K vyřešení této úlohy jsou potřebné tyto znalosti z matematiky:
geometrieplanimetrieJednotky fyzikálních veličinÚroveň náročnosti úkolu
Související a podobné příklady:
- Koeficient podobnosti
 Trojúhelníky ABC a A "B" C "jsou podobné koeficientem podobnosti 2. Velikosti úhlů trojúhelníku ABC jsou α = 35° a β = 48°. Urči velikosti všech úhlů trojúhelníku A" B "C".
Trojúhelníky ABC a A "B" C "jsou podobné koeficientem podobnosti 2. Velikosti úhlů trojúhelníku ABC jsou α = 35° a β = 48°. Urči velikosti všech úhlů trojúhelníku A" B "C". - Jsou podobné
 Trojúhelníky ABC a A'B'C 'jsou podobné s koeficientem podobnosti 2. Velikosti úhlů trojúhelníku ABC jsou alfa = 35°, beta = 48°. Urči velikosti všech úhlů trojúhelníku A'B'C '.
Trojúhelníky ABC a A'B'C 'jsou podobné s koeficientem podobnosti 2. Velikosti úhlů trojúhelníku ABC jsou alfa = 35°, beta = 48°. Urči velikosti všech úhlů trojúhelníku A'B'C '. - Trojúhelníky podobné
 Trojúhelníky ABC a A'B'C'. Jsou podobné. V trojúhelníku ABC jsou velikosti dvou úhlů 25 stupňů a 65 stupňů. Zdůvodni proč v trojúhelníku A'B'C' je součet velikosti dvou úhlů roven 90 stupňů.
Trojúhelníky ABC a A'B'C'. Jsou podobné. V trojúhelníku ABC jsou velikosti dvou úhlů 25 stupňů a 65 stupňů. Zdůvodni proč v trojúhelníku A'B'C' je součet velikosti dvou úhlů roven 90 stupňů. - Trojúhelníky podobné
 Pro trojúhelníky ABC a A'B'C' platí: alfa = alfa s čarou, beta s čarou = beta. a) jsou tyto trojúhelníky shodné? Proč? b) jsou tyto trojúhelníky podobné? Proč?
Pro trojúhelníky ABC a A'B'C' platí: alfa = alfa s čarou, beta s čarou = beta. a) jsou tyto trojúhelníky shodné? Proč? b) jsou tyto trojúhelníky podobné? Proč? - Úhly kosočtverce
 Pokud je jeden úhel v kosočtverci rovný 72,8°, jak velký je k němu sousední úhel kosočtverce?
Pokud je jeden úhel v kosočtverci rovný 72,8°, jak velký je k němu sousední úhel kosočtverce? - Úhel NOP v trojúhelníku
 Máme podobné trojúhelníky ABC s úhlem CAB=45° a úhlem ACB= 30° a podobný trojúhelník OPN. Jaký je úhel NOP na podobném trojúhelníku?
Máme podobné trojúhelníky ABC s úhlem CAB=45° a úhlem ACB= 30° a podobný trojúhelník OPN. Jaký je úhel NOP na podobném trojúhelníku? - Trojúhelník radiány
 Velikosti dvou vnitřní úhlů trojuhelníku ABC jsou α=6/18π and β=7/18π. Vypočítajte veľkosť tretieho uhla.
Velikosti dvou vnitřní úhlů trojuhelníku ABC jsou α=6/18π and β=7/18π. Vypočítajte veľkosť tretieho uhla.
