Příklady na trojúhelník - strana 59 z 124
Počet nalezených příkladů: 2480
- Pětiúhelník
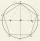 Uvnitř pravidelného pětiúhelníku ABCDE je bod P takový, že trojúhelník ABP je rovnostranný. Jak velký je úhel BCP? Udělej si náčrtek
Uvnitř pravidelného pětiúhelníku ABCDE je bod P takový, že trojúhelník ABP je rovnostranný. Jak velký je úhel BCP? Udělej si náčrtek - Střecha
 Střecha věže má tvar pravidelného čtyřbokého jehlanu, jehož podstavná hrana je dlouhá 11 m a boční stěna svírá s podstavou úhel velikosti 57°. Vypočtěte kolik krytiny potřebujeme na pokrytí celé střechy, pokud počítáme s 15% -ním odpadem.
Střecha věže má tvar pravidelného čtyřbokého jehlanu, jehož podstavná hrana je dlouhá 11 m a boční stěna svírá s podstavou úhel velikosti 57°. Vypočtěte kolik krytiny potřebujeme na pokrytí celé střechy, pokud počítáme s 15% -ním odpadem. - Stan
 Stan tvaru pravidelného čtyřbokého jehlanu má délku podstavné hrany a=2m a výšku v=1,8m. Kolik m² plátna potřebujeme na ušití stanu, musíme-li přidat 7% na švy? Kolik m³ bude ve stanu?
Stan tvaru pravidelného čtyřbokého jehlanu má délku podstavné hrany a=2m a výšku v=1,8m. Kolik m² plátna potřebujeme na ušití stanu, musíme-li přidat 7% na švy? Kolik m³ bude ve stanu? - Odvěsny
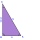 V pravoúhlém trojúhelníku jsou obsahy čtverců nad jeho stranami 169; 25 a 144. Délka jeho delší odvěsny je:
V pravoúhlém trojúhelníku jsou obsahy čtverců nad jeho stranami 169; 25 a 144. Délka jeho delší odvěsny je: - Střecha domu
 Střecha domu má tvar pravidelného čtyřbokého jehlanu s podstavnou hranou 13 m. Kolik m² je třeba na její pokrytí, jestliže sklon střechy 31° a na spoje a odpad počítáme 11% plechu navíc?
Střecha domu má tvar pravidelného čtyřbokého jehlanu s podstavnou hranou 13 m. Kolik m² je třeba na její pokrytí, jestliže sklon střechy 31° a na spoje a odpad počítáme 11% plechu navíc? - Cukrářka 2
 Cukrářka potřebuje z cukrářské hmoty ve tvaru koule o poloměru 25cm vyřezat ozdobu ve tvaru kužele. Určete poloměr podstavy ozdoby a (a výšku h) tak, aby se na výrobu ozdoby použilo co nejvíce hmoty.
Cukrářka potřebuje z cukrářské hmoty ve tvaru koule o poloměru 25cm vyřezat ozdobu ve tvaru kužele. Určete poloměr podstavy ozdoby a (a výšku h) tak, aby se na výrobu ozdoby použilo co nejvíce hmoty. - Kosmicka loď
 Kosmickou loď zpozorovalo radarové zařízení pod výškovým úhlem alpha = 34 stupňů 37 minut a od pozorovacího místa na Zemi měla vzdálenost u = 615km. Vypočítejte vzdálenost d kosmické lodi od Země v okamžiku pozorování. Zem považujeme za kouli s poloměrem
Kosmickou loď zpozorovalo radarové zařízení pod výškovým úhlem alpha = 34 stupňů 37 minut a od pozorovacího místa na Zemi měla vzdálenost u = 615km. Vypočítejte vzdálenost d kosmické lodi od Země v okamžiku pozorování. Zem považujeme za kouli s poloměrem - Z8–I–5 MO 2019
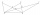 Pro osm navzájem různých bodů jako na obrázku platí, že body C, D, E leží na přímce rovnoběžné s přímkou AB, F je středem úsečky AD, G je středem úsečky AC a H je průsečíkem přímek AC a BE. Obsah trojúhelníku BCG je 12 cm² a obsah čtyřúhelníku DFHG je 8 c
Pro osm navzájem různých bodů jako na obrázku platí, že body C, D, E leží na přímce rovnoběžné s přímkou AB, F je středem úsečky AD, G je středem úsečky AC a H je průsečíkem přímek AC a BE. Obsah trojúhelníku BCG je 12 cm² a obsah čtyřúhelníku DFHG je 8 c - Součet velikostí hran
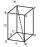 Vypočtěte povrch kvádru, je-li dán součet velikostí jeho hran a+b+c=19 cm a velikost tělesové úhlopříčky u=13 cm.
Vypočtěte povrch kvádru, je-li dán součet velikostí jeho hran a+b+c=19 cm a velikost tělesové úhlopříčky u=13 cm. - Plech 3
 Kolik m² pozinkovaného plechu se spotřebuje na pokrytí střechy věže, která má tvat čtyřbokohého jehlanu, jehož podstava hrany má délku 6m. Výška věže je 9m. Při pokrývání se počítá s 5 % odpadem plechu?
Kolik m² pozinkovaného plechu se spotřebuje na pokrytí střechy věže, která má tvat čtyřbokohého jehlanu, jehož podstava hrany má délku 6m. Výška věže je 9m. Při pokrývání se počítá s 5 % odpadem plechu? - Zmrzlinář
 Zmrzlinář Eda vymyslel nový hezký kornout tvaru pravidelného čtyřbokého jehlanu, v němž bude prodávat svoji zmrzlinu. Kornout bude mít délku boční hrany 5cm a stěnovou výšku 4cm. Aby mu ji mohli v továrně sériově vyrábět, potřebují ještě určit rozměry pod
Zmrzlinář Eda vymyslel nový hezký kornout tvaru pravidelného čtyřbokého jehlanu, v němž bude prodávat svoji zmrzlinu. Kornout bude mít délku boční hrany 5cm a stěnovou výšku 4cm. Aby mu ji mohli v továrně sériově vyrábět, potřebují ještě určit rozměry pod - Krabička
 Vypočítejte, kolik zaplatíme za papír na oblepení krabičky tvaru 3-bokého hranolu s podstavou pravoúhlého trojúhelníku, pokud odvěsny měří 12cm a 1,6dm, přepona měří 200mm. Krabička je vysoká 34cm. Za 1dm čtvereční papíru zaplatíme 0,13 €.
Vypočítejte, kolik zaplatíme za papír na oblepení krabičky tvaru 3-bokého hranolu s podstavou pravoúhlého trojúhelníku, pokud odvěsny měří 12cm a 1,6dm, přepona měří 200mm. Krabička je vysoká 34cm. Za 1dm čtvereční papíru zaplatíme 0,13 €. - Počet trojúhelníků
 Je dán čtverec ABCD a na každé jeho straně 4 vnitřních bodů. Určete počet všech trojúhelníků s vrcholy v těchto bodech.
Je dán čtverec ABCD a na každé jeho straně 4 vnitřních bodů. Určete počet všech trojúhelníků s vrcholy v těchto bodech. - Trojboký hranol
 Rovina, která prochází hranou AB a středem hrany CC' pravidelného trojbokého hranolu ABCA'B'C', svírá s podstavou úhel 46 stupňů, |AB| = 12 cm. Vypočítejte objem hranolu.
Rovina, která prochází hranou AB a středem hrany CC' pravidelného trojbokého hranolu ABCA'B'C', svírá s podstavou úhel 46 stupňů, |AB| = 12 cm. Vypočítejte objem hranolu. - Síly
 Na bod T působí tři navzájem kolmé síly F1 = 18 N, F2 = 16 N, F3 = 4 N. Určete výslednici F a úhly, které svírá výslednice se složkami F1, F2, F3.
Na bod T působí tři navzájem kolmé síly F1 = 18 N, F2 = 16 N, F3 = 4 N. Určete výslednici F a úhly, které svírá výslednice se složkami F1, F2, F3. - Šestiúhelník lomeno
 Pravidelný šestiúhelník rozdělte úsečkami na devět zcela shodných dílů; žádný z nich nesmí být v zrcadlovém zobrazení (jednotlivé díly mohou být pouze libovolně pootočeny).
Pravidelný šestiúhelník rozdělte úsečkami na devět zcela shodných dílů; žádný z nich nesmí být v zrcadlovém zobrazení (jednotlivé díly mohou být pouze libovolně pootočeny). - Ortocentrum
 Je dán trojúhelník ABC: A (-1,3), B(2,-2), C(-4,-3). Urči souřadnice průsečíku výšek a souřadnice průsečík os stran.
Je dán trojúhelník ABC: A (-1,3), B(2,-2), C(-4,-3). Urči souřadnice průsečíku výšek a souřadnice průsečík os stran. - V rovině
 V rovině jsou dány 3 různé body C, E, F. Dorýsuj prosím čtverec ABCD, když E, F leží na úhlopříčkách tohoto čtverce. Kolik má úloha řešení? Děkuji
V rovině jsou dány 3 různé body C, E, F. Dorýsuj prosím čtverec ABCD, když E, F leží na úhlopříčkách tohoto čtverce. Kolik má úloha řešení? Děkuji - Do kterého
 Do kterého ze sáčků ve tvaru pláště rotačního kužele se vejde větší množství pražené kukuřice? První sáček má výšku 20 cm a délka jeho strany je 24 cm, druhý sáček má poloměr podstavy 10 cm a výšku 25 cm.
Do kterého ze sáčků ve tvaru pláště rotačního kužele se vejde větší množství pražené kukuřice? První sáček má výšku 20 cm a délka jeho strany je 24 cm, druhý sáček má poloměr podstavy 10 cm a výšku 25 cm. - Střecha
 Střecha kostelní věže má tvar pravidelného čtyřbokého jehlanu s podstavnou hranou délky 5,4m a výškou 5m. Bylo zjištěno, že bude třeba opravit 27% krytiny na střešní ploše. Jaké množství materiálu bude třeba?
Střecha kostelní věže má tvar pravidelného čtyřbokého jehlanu s podstavnou hranou délky 5,4m a výškou 5m. Bylo zjištěno, že bude třeba opravit 27% krytiny na střešní ploše. Jaké množství materiálu bude třeba?
Máš příklad z matematiky, který jsi tady nenašel vyřešený? Pošli nám příklad a my Ti ho zkusíme vypočítat.
